Number of replications

Learning objectives:

  • Understand how the confidence interval method can be used to choose an appropriate number of replications to run.
  • Learn how to implement this manually or using an automated method.

Pre-reading:

This page continues on from: Replications.

Entity generation → Entity processing → Initialisation bias → Performance measures → Replications → Number of replications

Required packages:

These should be available from environment setup in the “Test yourself” section of Environments.

from IPython.display import HTML
from itables import to_html_datatable
import numpy as np
import pandas as pd
import scipy.stats as st
import simpy
from sim_tools.distributions import Exponential
from sim_tools.output_analysis import (
    confidence_interval_method,
    plotly_confidence_interval_method,
    ReplicationsAlgorithm
)
from typing import Protocol, runtime_checkable
library(dplyr)
library(kableExtra)
library(knitr)
library(R6)
library(simmer)
library(tidyr)



When running your simulation model, each replication will give a slightly different result because of randomness. To get a reliable estimate of any performance measure (such as average waiting time), you run the simulation multiple times and take the average across all these runs.

How many replications should you run? If you run too few, your average could jump around alot with varying seeds, making your result unstable and unreliable. If you run too many, it will take a long time and use more computing resources than needed. To find a sensible balance, we can use the confidence interval method.

Choice of an appropriate number of replications forms part of your model experimentation validation (see verification and validation page).

Confidence interval method

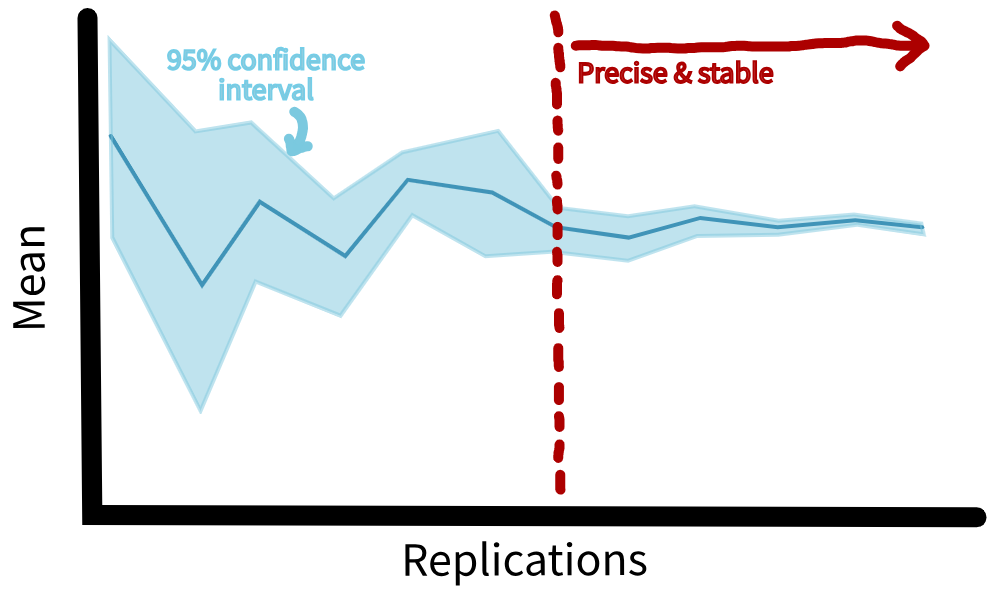
When finding the average result across several simulation runs, you can also calculate a confidence interval. This is a measure of variation which shows the range where your true average result is likely to fall. You should choose a suitable confidence level (typically 95%).

Then, run your simulation for an increasing number of replications. At first, this confidence interval might jump around as different replication produce varying results. However, after enough runs, the interval will settle into a stable and narrow range. At this point, you can assume that adding more runs probably wouldn’t change your answer by much.


When selecting the number of replications you should repeat the analysis for all performance measures and select the highest value as your number of replications.

We’ll show two ways of implementing this: manually and automated.

Simulation code

The simulation being used is that from the Replications page.

Note

On this page, we will use a longer warm-up and run length than the short illustrative values used earlier (i.e., 30 minute warm-up, 40 minute data collection).

We are not using the previously determined warm-up length, but have simply chosen reasonably long values for this example. Very short runs, like 30/40 minutes, will be unstable and need many replications to achieve reliable outcomes.

As before, these assumptions are for demonstration only, and in later examples we will return to the shorter parameter settings for simplicity.

Manual inspection

To begin, we run our simulation model for multiple replications using our usual workflow. Here, we have set to run for 50 replications.

For this analysis, we are interested in the mean results from each replication (result["run"]).

# Run simulation for multiple replications
runner = Runner(param=Parameters(warm_up_period=10000,
                                 data_collection_period=10000,
                                 number_of_runs=50))
result = runner.run_reps()
HTML(to_html_datatable(result["run"]))
Loading ITables v2.5.2 from the internet... (need help?)


We pass these results to the confidence_interval_method function from the sim-tools package.

The desired_precision parameter is set to 0.1, which means we are interested in identifying when the percentage deviation of the confidence interval from the mean falls below 10%. Note: This threshold is our default but relatively arbitrary. We are just using it to help us identify the point where results are stable enough.

# Define metrics to inspect
metrics = ["mean_wait_time", "mean_utilisation_tw", "mean_queue_length",
           "mean_time_in_system", "mean_patients_in_system"]

# Run the confidence interval method
confint_results = confidence_interval_method(
    replications=result["run"][metrics],
    desired_precision=0.1,
    min_rep=5,
    decimal_places=6
)


For each metric, the function returns:

  1. The number of replications required for deviation to fall below 10% (and must also be higher than min_rep set in confidence_interval_method()).
  2. A dataframe of cumulative calculations: the mean, cumulative mean, standard deviation, confidence interval bounds, and the percentage deviation of the confidence interval from the mean (displayed in the far-right column).
print(confint_results["mean_wait_time"][0])
24
HTML(to_html_datatable(confint_results["mean_wait_time"][1]))
Loading ITables v2.5.2 from the internet... (need help?) 
print(confint_results["mean_utilisation_tw"][0])
6
HTML(to_html_datatable(confint_results["mean_utilisation_tw"][1]))
Loading ITables v2.5.2 from the internet... (need help?) 
print(confint_results["mean_queue_length"][0])
24
HTML(to_html_datatable(confint_results["mean_queue_length"][1]))
Loading ITables v2.5.2 from the internet... (need help?) 
print(confint_results["mean_time_in_system"][0])
9
HTML(to_html_datatable(confint_results["mean_time_in_system"][1]))
Loading ITables v2.5.2 from the internet... (need help?) 
print(confint_results["mean_patients_in_system"][0])
9
HTML(to_html_datatable(confint_results["mean_patients_in_system"][1]))
Loading ITables v2.5.2 from the internet... (need help?)


To visualise when precision is achieved and check for stability, we can use the plotly_confidence_interval_method function from sim-tools:

p = plotly_confidence_interval_method(
    n_reps=confint_results["mean_wait_time"][0],
    conf_ints=confint_results["mean_wait_time"][1],
    metric_name="Mean Wait Time")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=confint_results["mean_utilisation_tw"][0],
    conf_ints=confint_results["mean_utilisation_tw"][1],
    metric_name="Mean Utilisation")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=confint_results["mean_queue_length"][0],
    conf_ints=confint_results["mean_queue_length"][1],
    metric_name="Mean Queue Length")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=confint_results["mean_time_in_system"][0],
    conf_ints=confint_results["mean_time_in_system"][1],
    metric_name="Mean Time In System")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=confint_results["mean_patients_in_system"][0],
    conf_ints=confint_results["mean_patients_in_system"][1],
    metric_name="Mean Patients In System")
p.update_layout(autosize=True, width=None, height=390)

For this analysis, we have created two functions confidence_interval_method and plot_replication_ci.

#' Use the confidence interval method to select the number of replications.
#'
#' This could be altered to use WelfordStats and ReplicationTabuliser if
#' desired, but currently is independent.
#'
#' @param param List of parameters for the model.
#' @param desired_precision Desired mean deviation from confidence interval.
#' @param metric Name of performance metric to assess.
#' @param verbose Boolean, whether to print messages about parameters.
#'
#' @importFrom rlang .data
#' @importFrom utils tail
#'
#' @return Dataframe with results from each replication.
#' @export

confidence_interval_method <- function(
  param, desired_precision, metric, verbose = TRUE
) {
  # Run model for specified number of replications
  if (isTRUE(verbose)) {
    print(param)
  }
  results <- runner(param = param)[["run_results"]]

  # Initialise list to store the results
  cumulative_list <- list()

  # For each row in the dataframe, filter to rows up to the i-th replication
  # then perform calculations
  for (i in 1L:param[["number_of_runs"]]) {

    # Filter rows up to the i-th replication
    subset_data <- results[[metric]][1L:i]

    # Get latest data point
    last_data_point <- tail(subset_data, n = 1L)

    # Calculate mean
    mean_value <- mean(subset_data)

    # Some calculations require a few observations else will error...
    if (i < 3L) {
      # When only one observation, set to NA
      stdev <- NA
      lower_ci <- NA
      upper_ci <- NA
      deviation <- NA
    } else {
      # Else, calculate standard deviation, 95% confidence interval, and
      # percentage deviation
      stdev <- stats::sd(subset_data)
      ci <- stats::t.test(subset_data)[["conf.int"]]
      lower_ci <- ci[[1L]]
      upper_ci <- ci[[2L]]
      deviation <- ((upper_ci - mean_value) / mean_value)
    }

    # Append to the cumulative list
    cumulative_list[[i]] <- data.frame(
      replications = i,
      data = last_data_point,
      cumulative_mean = mean_value,
      stdev = stdev,
      lower_ci = lower_ci,
      upper_ci = upper_ci,
      deviation = deviation
    )
  }

  # Combine the list into a single data frame
  cumulative <- do.call(rbind, cumulative_list)
  cumulative[["metric"]] <- metric

  # Get the minimum number of replications where deviation is less than target
  compare <- dplyr::filter(
    cumulative, .data[["deviation"]] <= desired_precision
  )
  if (nrow(compare) > 0L) {
    # Get minimum number
    n_reps <- compare |>
      dplyr::slice_head() |>
      dplyr::select(replications) |>
      dplyr::pull()
    message("Reached desired precision (", desired_precision, ") in ",
            n_reps, " replications.")
  } else {
    warning("Running ", param[["number_of_runs"]], " replications did not ",
            "reach desired precision (", desired_precision, ").",
            call. = FALSE)
  }
  cumulative
}
#' Generate a plot of metric and confidence intervals with increasing
#' simulation replications
#'
#' @param conf_ints A dataframe containing confidence interval statistics,
#' including cumulative mean, upper/lower bounds, and deviations. As returned
#' by ReplicationTabuliser summary_table() method.
#' @param yaxis_title Label for y axis.
#' @param file_path Path and filename to save the plot to.
#' @param min_rep The number of replications required to meet the desired
#' precision.
#'
#' @return A ggplot object if file_path is NULL; otherwise, the plot is saved
#' to file and NULL is returned invisibly.
#' @export

plot_replication_ci <- function(
  conf_ints, yaxis_title, file_path = NULL, min_rep = NULL
) {
  # Plot the cumulative mean and confidence interval
  p <- ggplot2::ggplot(conf_ints,
                       ggplot2::aes(x = .data[["replications"]],
                                    y = .data[["cumulative_mean"]])) +
    ggplot2::geom_line() +
    ggplot2::geom_ribbon(
      ggplot2::aes(ymin = .data[["lower_ci"]], ymax = .data[["upper_ci"]]),
      alpha = 0.2
    )

  # If specified, plot the minimum suggested number of replications
  if (!is.null(min_rep)) {
    p <- p +
      ggplot2::geom_vline(
        xintercept = min_rep, linetype = "dashed", color = "red"
      )
  }

  # Modify labels and style
  p <- p +
    ggplot2::labs(x = "Replications", y = yaxis_title) +
    ggplot2::theme_minimal()

  # Save the plot
  if (!is.null(file_path)) {
    ggplot2::ggsave(filename = file_path,
                    width = 6.5, height = 4L, bg = "white")
  } else {
    p
  }
}
metrics <- c("mean_wait_time_doctor", "utilisation_doctor",
             "mean_queue_length_doctor", "mean_time_in_system",
             "mean_patients_in_system")

ci_df <- list()
for (m in metrics) {
  ci_df[[m]] <- confidence_interval_method(
    param = create_params(warm_up_period = 10000L,
                          data_collection_period = 10000L,
                          number_of_runs = 50L),
    desired_precision = 0.1,
    metric = m,
    verbose = FALSE
  )
}
Reached desired precision (0.1) in 18 replications.
Reached desired precision (0.1) in 3 replications.
Reached desired precision (0.1) in 19 replications.
Reached desired precision (0.1) in 3 replications.
Reached desired precision (0.1) in 6 replications.
ci_df[["mean_wait_time_doctor"]] |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 5.667672 5.667672 NA NA NA NA mean_wait_time_doctor
2 5.328368 5.498020 NA NA NA NA mean_wait_time_doctor
3 4.934004 5.310015 0.3671783 4.397893 6.222136 0.1717738 mean_wait_time_doctor
4 3.671831 4.900469 0.8722335 3.512551 6.288387 0.2832215 mean_wait_time_doctor
5 3.412813 4.602938 1.0065869 3.353095 5.852780 0.2715315 mean_wait_time_doctor
6 5.059963 4.679109 0.9194487 3.714206 5.644011 0.2062150 mean_wait_time_doctor
7 4.842750 4.702486 0.8416138 3.924123 5.480849 0.1655216 mean_wait_time_doctor
8 4.862139 4.722443 0.7812248 4.069322 5.375563 0.1383014 mean_wait_time_doctor
9 4.667285 4.716314 0.7310001 4.154418 5.278210 0.1191389 mean_wait_time_doctor
10 6.072426 4.851925 0.8117215 4.271255 5.432596 0.1196784 mean_wait_time_doctor
11 4.269149 4.798946 0.7898594 4.268311 5.329580 0.1105732 mean_wait_time_doctor
12 3.412673 4.683423 0.8528233 4.141565 5.225281 0.1156970 mean_wait_time_doctor
13 4.891019 4.699392 0.8185437 4.204751 5.194033 0.1052564 mean_wait_time_doctor
14 3.492198 4.613164 0.8500401 4.122365 5.103962 0.1063909 mean_wait_time_doctor
15 3.890397 4.564979 0.8401085 4.099743 5.030216 0.1019143 mean_wait_time_doctor
16 2.990553 4.466578 0.9020290 3.985920 4.947235 0.1076120 mean_wait_time_doctor
17 5.359595 4.519108 0.8998408 4.056452 4.981763 0.1023776 mean_wait_time_doctor
18 3.888761 4.484089 0.8855267 4.043727 4.924451 0.0982055 mean_wait_time_doctor
19 3.689211 4.442253 0.8796859 4.018258 4.866248 0.0954459 mean_wait_time_doctor
20 4.288418 4.434561 0.8569141 4.033513 4.835610 0.0904369 mean_wait_time_doctor
21 4.359718 4.430997 0.8353762 4.050739 4.811256 0.0858179 mean_wait_time_doctor
22 3.882755 4.406077 0.8235803 4.040922 4.771232 0.0828753 mean_wait_time_doctor
23 4.639772 4.416238 0.8061191 4.067646 4.764830 0.0789342 mean_wait_time_doctor
24 3.956291 4.397074 0.7939705 4.061809 4.732338 0.0762472 mean_wait_time_doctor
25 4.254914 4.391387 0.7777733 4.070338 4.712436 0.0731088 mean_wait_time_doctor
26 4.701406 4.403311 0.7644807 4.094531 4.712091 0.0701246 mean_wait_time_doctor
27 5.532829 4.445145 0.7805157 4.136383 4.753907 0.0694604 mean_wait_time_doctor
28 5.432689 4.480414 0.7883348 4.174730 4.786099 0.0682268 mean_wait_time_doctor
29 4.290552 4.473867 0.7749318 4.179099 4.768636 0.0658867 mean_wait_time_doctor
30 3.302238 4.434813 0.7909292 4.139475 4.730151 0.0665953 mean_wait_time_doctor
31 3.791986 4.414077 0.7861594 4.125711 4.702442 0.0653286 mean_wait_time_doctor
32 3.405390 4.382555 0.7936654 4.096408 4.668702 0.0652923 mean_wait_time_doctor
33 3.714474 4.362310 0.7897756 4.082268 4.642353 0.0641959 mean_wait_time_doctor
34 4.399654 4.363409 0.7777436 4.092041 4.634776 0.0621917 mean_wait_time_doctor
35 5.318725 4.390703 0.7830515 4.121716 4.659691 0.0612630 mean_wait_time_doctor
36 6.269489 4.442892 0.8328874 4.161083 4.724700 0.0634291 mean_wait_time_doctor
37 6.217519 4.490855 0.8715206 4.200275 4.781434 0.0647047 mean_wait_time_doctor
38 4.550575 4.492426 0.8597173 4.209844 4.775008 0.0629019 mean_wait_time_doctor
39 4.366934 4.489209 0.8485677 4.214135 4.764283 0.0612745 mean_wait_time_doctor
40 3.594789 4.466848 0.8494726 4.195174 4.738523 0.0608202 mean_wait_time_doctor
41 4.340154 4.463758 0.8390203 4.198931 4.728586 0.0593284 mean_wait_time_doctor
42 5.209670 4.481518 0.8366795 4.220790 4.742246 0.0581784 mean_wait_time_doctor
43 3.739431 4.464260 0.8343692 4.207479 4.721041 0.0575193 mean_wait_time_doctor
44 4.902840 4.474228 0.8272567 4.222719 4.725737 0.0562128 mean_wait_time_doctor
45 3.445952 4.451377 0.8320438 4.201403 4.701351 0.0561565 mean_wait_time_doctor
46 3.791042 4.437022 0.8284876 4.190992 4.683052 0.0554495 mean_wait_time_doctor
47 4.572846 4.439912 0.8196723 4.199247 4.680577 0.0542049 mean_wait_time_doctor
48 5.344848 4.458765 0.8213576 4.220267 4.697262 0.0534896 mean_wait_time_doctor
49 3.817683 4.445681 0.8179004 4.210753 4.680610 0.0528442 mean_wait_time_doctor
50 4.078986 4.438347 0.8111708 4.207815 4.668880 0.0519410 mean_wait_time_doctor 
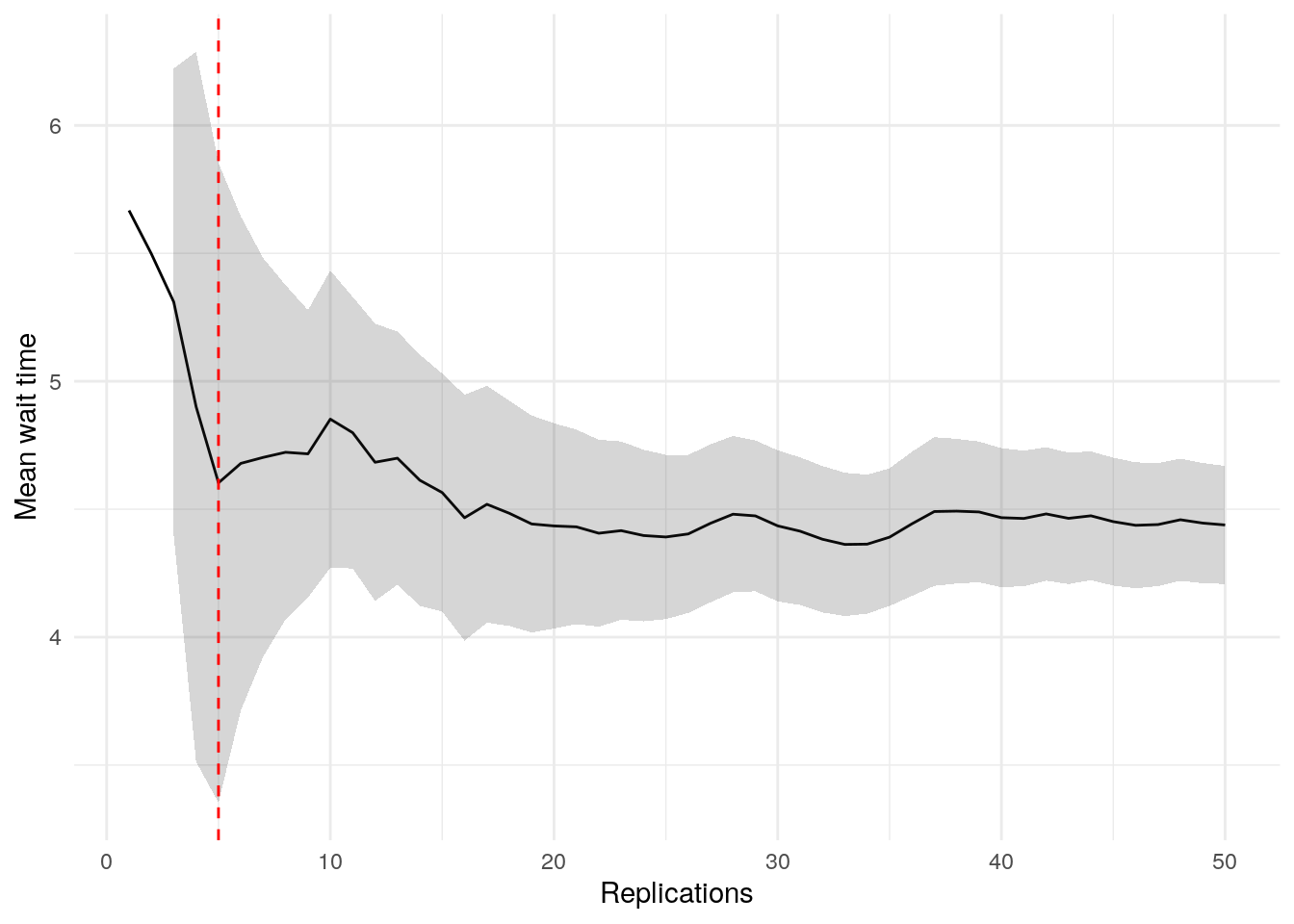
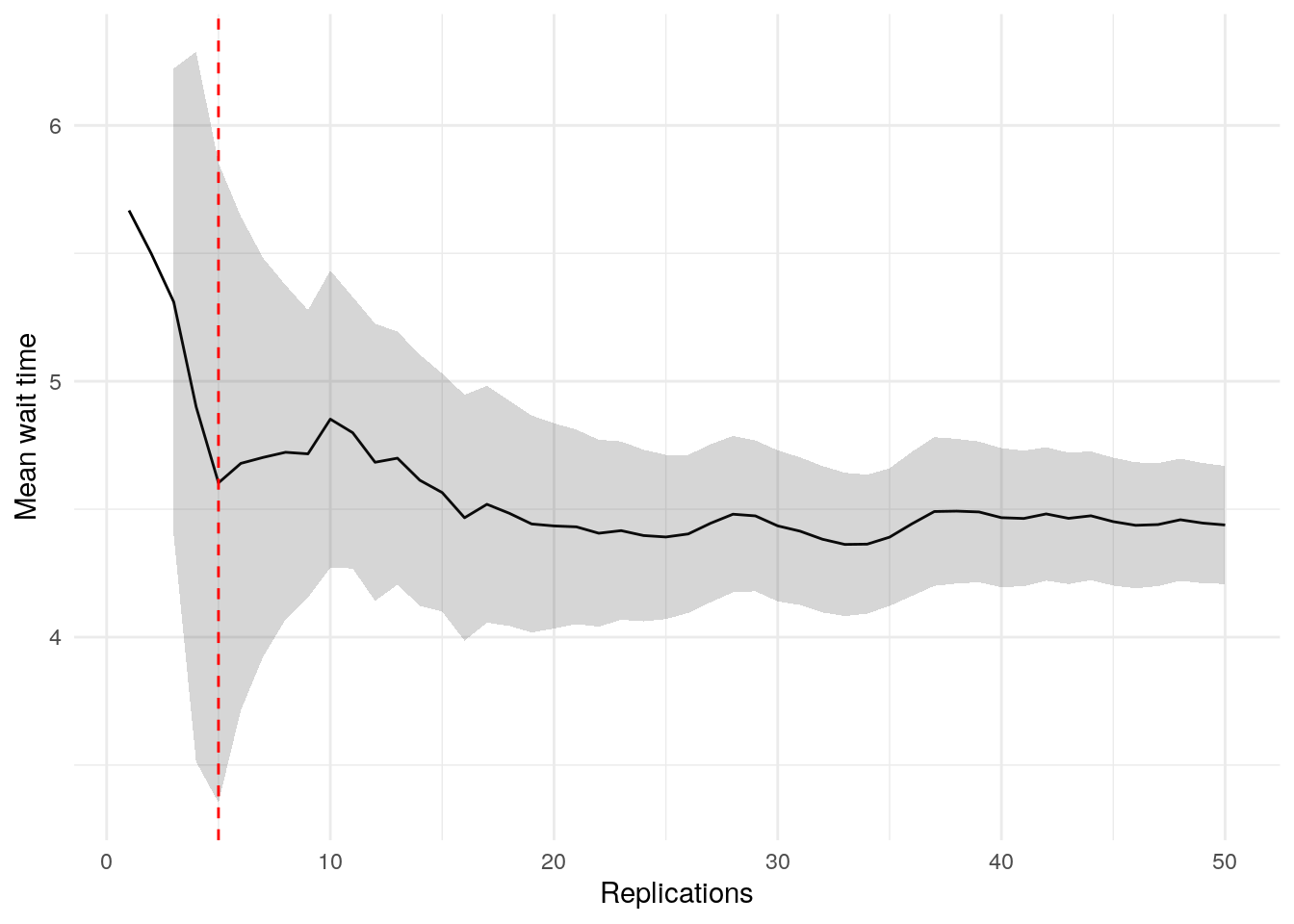
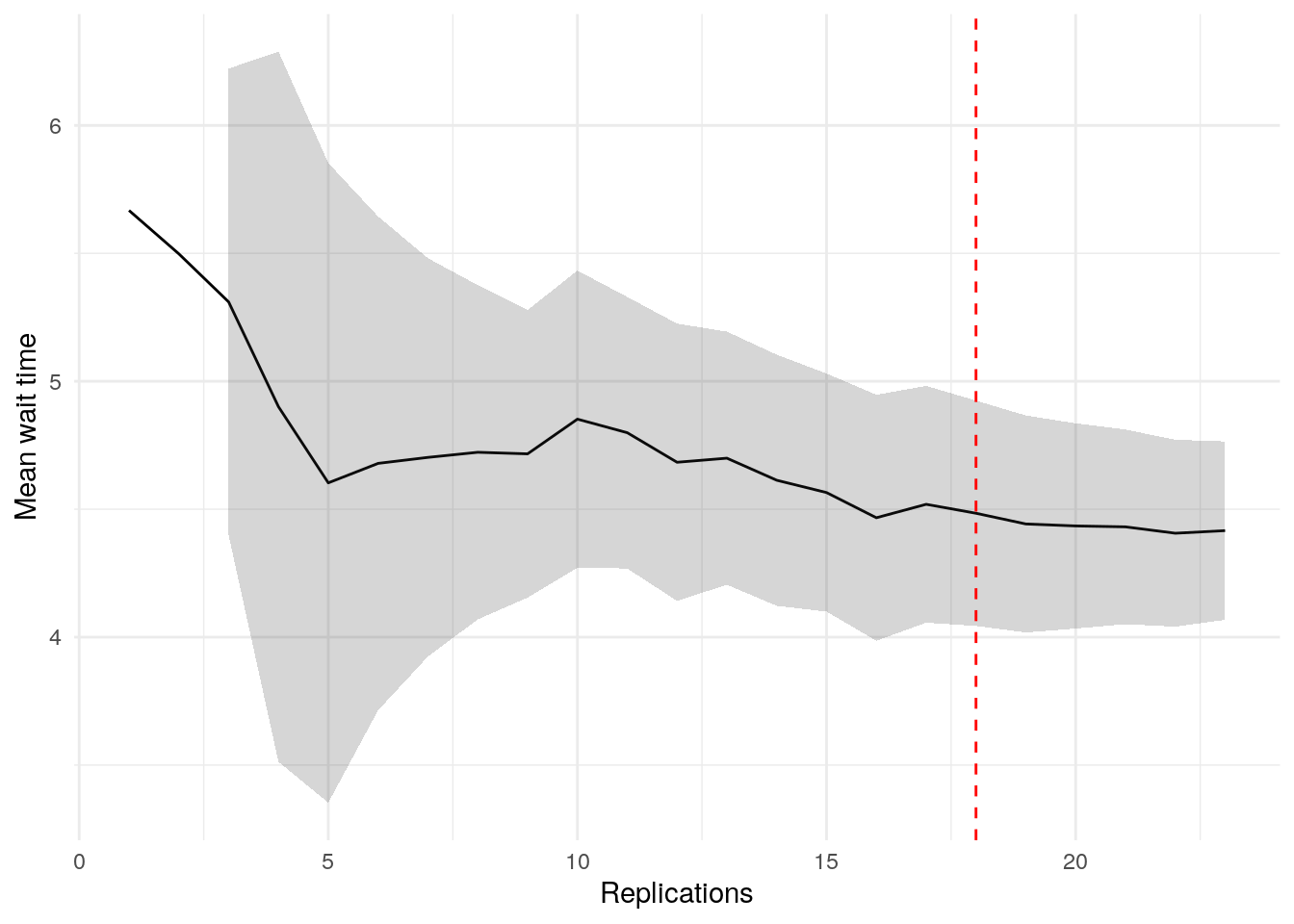
plot_replication_ci(
  conf_ints = ci_df[["mean_wait_time_doctor"]],
  yaxis_title = "Mean wait time",
  min_rep = 5L
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

ci_df[["utilisation_doctor"]] |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 0.6832362 0.6832362 NA NA NA NA utilisation_doctor
2 0.7014341 0.6923351 NA NA NA NA utilisation_doctor
3 0.6503975 0.6783559 0.0258659 0.6141014 0.7426104 0.0947210 utilisation_doctor
4 0.6437990 0.6697167 0.0272869 0.6262971 0.7131363 0.0648327 utilisation_doctor
5 0.6789189 0.6715571 0.0239868 0.6417735 0.7013407 0.0443500 utilisation_doctor
6 0.6713653 0.6715251 0.0214546 0.6490099 0.6940404 0.0335285 utilisation_doctor
7 0.6775094 0.6723800 0.0197155 0.6541463 0.6906138 0.0271182 utilisation_doctor
8 0.6528520 0.6699390 0.0195151 0.6536240 0.6862541 0.0243530 utilisation_doctor
9 0.6541008 0.6681792 0.0190028 0.6535724 0.6827861 0.0218607 utilisation_doctor
10 0.6893232 0.6702936 0.0191230 0.6566138 0.6839734 0.0204087 utilisation_doctor
11 0.6477562 0.6682448 0.0193726 0.6552301 0.6812594 0.0194759 utilisation_doctor
12 0.6335263 0.6653516 0.0210149 0.6519993 0.6787038 0.0200680 utilisation_doctor
13 0.6503795 0.6641999 0.0205443 0.6517851 0.6766147 0.0186913 utilisation_doctor
14 0.6284034 0.6616430 0.0219347 0.6489783 0.6743077 0.0191413 utilisation_doctor
15 0.6647776 0.6618519 0.0211523 0.6501382 0.6735657 0.0176984 utilisation_doctor
16 0.6282434 0.6597514 0.0220949 0.6479779 0.6715250 0.0178454 utilisation_doctor
17 0.6814358 0.6610270 0.0220303 0.6497000 0.6723539 0.0171354 utilisation_doctor
18 0.6703249 0.6615435 0.0214846 0.6508595 0.6722276 0.0161502 utilisation_doctor
19 0.6278075 0.6597679 0.0222676 0.6490353 0.6705006 0.0162673 utilisation_doctor
20 0.6750253 0.6605308 0.0219405 0.6502623 0.6707993 0.0155458 utilisation_doctor
21 0.6663518 0.6608080 0.0214227 0.6510565 0.6705595 0.0147569 utilisation_doctor
22 0.6746140 0.6614355 0.0211126 0.6520747 0.6707963 0.0141522 utilisation_doctor
23 0.6796506 0.6622275 0.0209739 0.6531577 0.6712973 0.0136959 utilisation_doctor
24 0.6635614 0.6622831 0.0205147 0.6536205 0.6709457 0.0130799 utilisation_doctor
25 0.6439847 0.6615511 0.0204135 0.6531249 0.6699774 0.0127372 utilisation_doctor
26 0.6548798 0.6612946 0.0200438 0.6531987 0.6693904 0.0122425 utilisation_doctor
27 0.6608308 0.6612774 0.0196548 0.6535022 0.6690526 0.0117578 utilisation_doctor
28 0.6865314 0.6621793 0.0198691 0.6544749 0.6698837 0.0116349 utilisation_doctor
29 0.6431757 0.6615240 0.0198276 0.6539820 0.6690660 0.0114010 utilisation_doctor
30 0.6628206 0.6615672 0.0194842 0.6542917 0.6688427 0.0109974 utilisation_doctor
31 0.6217329 0.6602823 0.0204491 0.6527815 0.6677830 0.0113600 utilisation_doctor
32 0.6519350 0.6600214 0.0201706 0.6527491 0.6672937 0.0110182 utilisation_doctor
33 0.6551604 0.6598741 0.0198710 0.6528282 0.6669200 0.0106777 utilisation_doctor
34 0.6686245 0.6601315 0.0196250 0.6532840 0.6669790 0.0103729 utilisation_doctor
35 0.6902273 0.6609913 0.0199923 0.6541237 0.6678590 0.0103899 utilisation_doctor
36 0.6739451 0.6613512 0.0198226 0.6546442 0.6680582 0.0101414 utilisation_doctor
37 0.6806258 0.6618721 0.0198005 0.6552703 0.6684739 0.0099745 utilisation_doctor
38 0.6504647 0.6615719 0.0196186 0.6551234 0.6680204 0.0097472 utilisation_doctor
39 0.6712074 0.6618190 0.0194201 0.6555237 0.6681142 0.0095121 utilisation_doctor
40 0.6725828 0.6620881 0.0192449 0.6559333 0.6682429 0.0092961 utilisation_doctor
41 0.6568020 0.6619591 0.0190208 0.6559555 0.6679628 0.0090696 utilisation_doctor
42 0.6883579 0.6625877 0.0192239 0.6565971 0.6685783 0.0090412 utilisation_doctor
43 0.6484279 0.6622584 0.0191160 0.6563754 0.6681414 0.0088833 utilisation_doctor
44 0.6631406 0.6622784 0.0188929 0.6565345 0.6680224 0.0086730 utilisation_doctor
45 0.6412090 0.6618102 0.0189392 0.6561203 0.6675002 0.0085976 utilisation_doctor
46 0.6604320 0.6617803 0.0187287 0.6562185 0.6673420 0.0084042 utilisation_doctor
47 0.6436991 0.6613956 0.0187108 0.6559019 0.6668893 0.0083062 utilisation_doctor
48 0.6934467 0.6620633 0.0190800 0.6565230 0.6676036 0.0083682 utilisation_doctor
49 0.6702343 0.6622300 0.0189163 0.6567967 0.6676634 0.0082047 utilisation_doctor
50 0.6737071 0.6624596 0.0187925 0.6571188 0.6678004 0.0080620 utilisation_doctor 
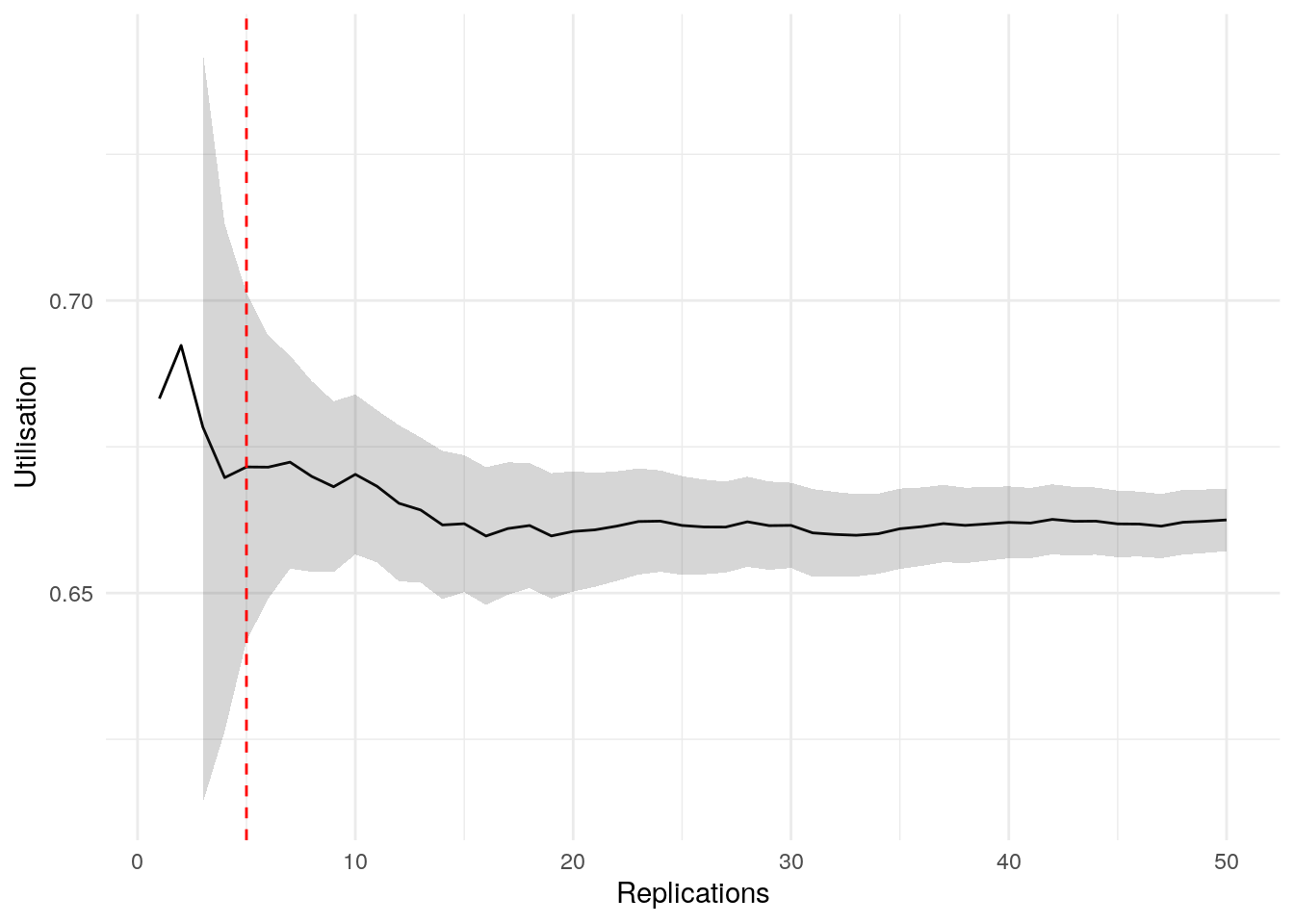
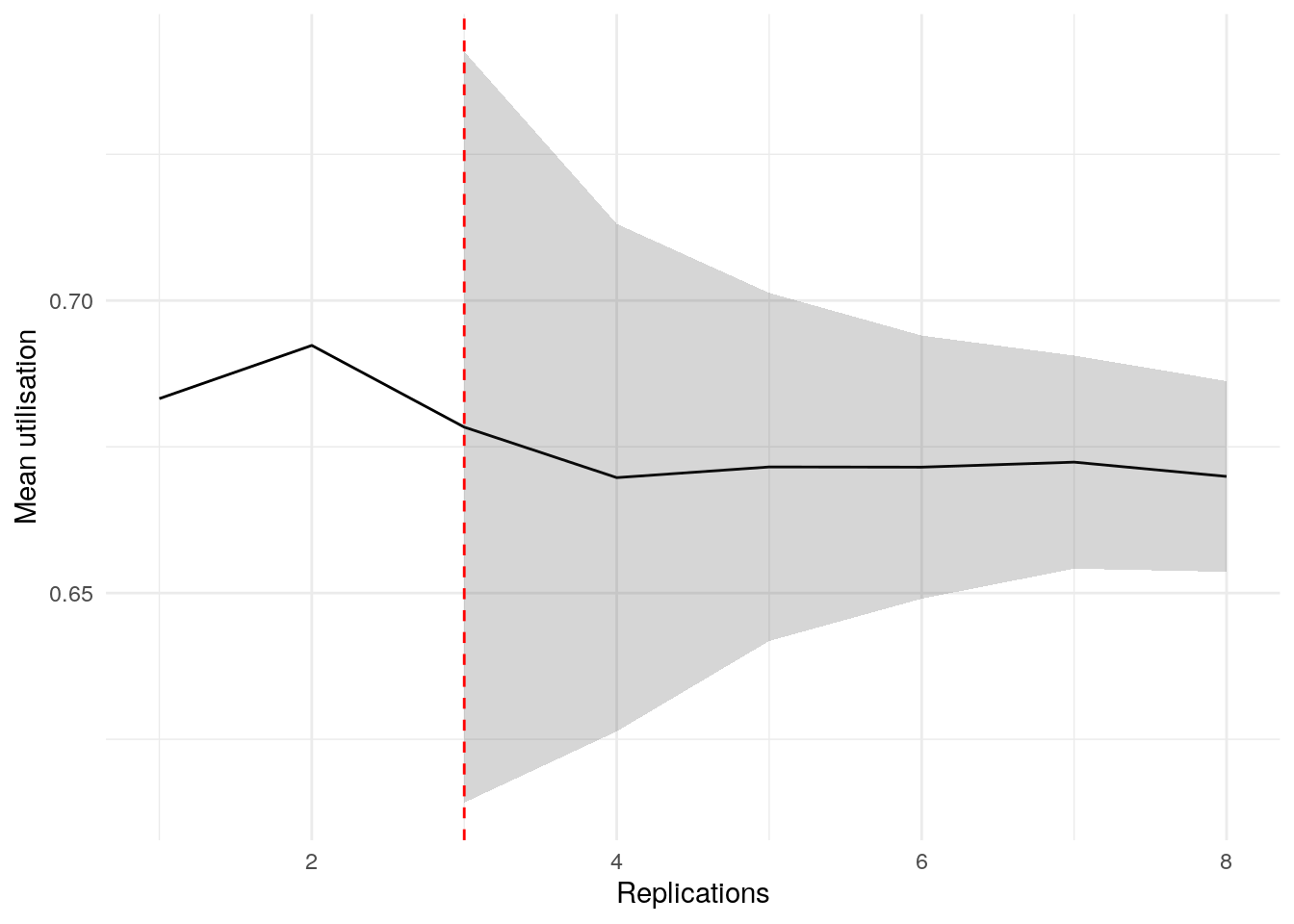
plot_replication_ci(
  conf_ints = ci_df[["utilisation_doctor"]],
  yaxis_title = "Utilisation",
  min_rep = 5L
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

ci_df[["mean_queue_length_doctor"]] |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 1.2047321 1.2047321 NA NA NA NA mean_queue_length_doctor
2 1.0585763 1.1316542 NA NA NA NA mean_queue_length_doctor
3 1.0061322 1.0898135 0.1029189 0.8341487 1.3454783 0.2345950 mean_queue_length_doctor
4 0.7220796 0.9978800 0.2021598 0.6761987 1.3195614 0.3223648 mean_queue_length_doctor
5 0.7147191 0.9412479 0.2160728 0.6729580 1.2095377 0.2850363 mean_queue_length_doctor
6 0.9998528 0.9510153 0.1947367 0.7466517 1.1553790 0.2148900 mean_queue_length_doctor
7 0.9630582 0.9527358 0.1778278 0.7882725 1.1171990 0.1726221 mean_queue_length_doctor
8 0.9401393 0.9511612 0.1646967 0.8134713 1.0888511 0.1447598 mean_queue_length_doctor
9 0.9319599 0.9490277 0.1541926 0.8305048 1.0675506 0.1248888 mean_queue_length_doctor
10 1.2095963 0.9750846 0.1671025 0.8555466 1.0946225 0.1225924 mean_queue_length_doctor
11 0.8724811 0.9657570 0.1615177 0.8572479 1.0742660 0.1123565 mean_queue_length_doctor
12 0.6465119 0.9391532 0.1794699 0.8251235 1.0531830 0.1214176 mean_queue_length_doctor
13 0.9578633 0.9405925 0.1719077 0.8367097 1.0444752 0.1104440 mean_queue_length_doctor
14 0.7166333 0.9245954 0.1756750 0.8231637 1.0260271 0.1097039 mean_queue_length_doctor
15 0.7937702 0.9158737 0.1726219 0.8202789 1.0114685 0.1043755 mean_queue_length_doctor
16 0.5950870 0.8958245 0.1850493 0.7972187 0.9944304 0.1100727 mean_queue_length_doctor
17 1.0952642 0.9075563 0.1855878 0.8121358 1.0029767 0.1051400 mean_queue_length_doctor
18 0.7925600 0.9011676 0.1820754 0.8106236 0.9917116 0.1004741 mean_queue_length_doctor
19 0.7424607 0.8928146 0.1806527 0.8057428 0.9798864 0.0975251 mean_queue_length_doctor
20 0.8539327 0.8908705 0.1760492 0.8084769 0.9732641 0.0924866 mean_queue_length_doctor
21 0.8341843 0.8881712 0.1720368 0.8098609 0.9664814 0.0881702 mean_queue_length_doctor
22 0.7866429 0.8835562 0.1692804 0.8085015 0.9586110 0.0849462 mean_queue_length_doctor
23 0.9277437 0.8854774 0.1656448 0.8138472 0.9571076 0.0808944 mean_queue_length_doctor
24 0.7972331 0.8818006 0.1630022 0.8129708 0.9506304 0.0780559 mean_queue_length_doctor
25 0.8530547 0.8806507 0.1596737 0.8147407 0.9465608 0.0748424 mean_queue_length_doctor
26 0.9224187 0.8822572 0.1566619 0.8189801 0.9455343 0.0717219 mean_queue_length_doctor
27 1.1294072 0.8914109 0.1608146 0.8277948 0.9550270 0.0713657 mean_queue_length_doctor
28 1.0772452 0.8980478 0.1616690 0.8353591 0.9607366 0.0698055 mean_queue_length_doctor
29 0.8531167 0.8964985 0.1589749 0.8360277 0.9569693 0.0674522 mean_queue_length_doctor
30 0.6787016 0.8892386 0.1611916 0.8290487 0.9494285 0.0676870 mean_queue_length_doctor
31 0.7243055 0.8839182 0.1612270 0.8247796 0.9430567 0.0669050 mean_queue_length_doctor
32 0.6910776 0.8778919 0.1622274 0.8194027 0.9363811 0.0666246 mean_queue_length_doctor
33 0.7121484 0.8728694 0.1622583 0.8153351 0.9304037 0.0659140 mean_queue_length_doctor
34 0.9340725 0.8746695 0.1601253 0.8187991 0.9305398 0.0638760 mean_queue_length_doctor
35 1.1099986 0.8813932 0.1626908 0.8255069 0.9372794 0.0634067 mean_queue_length_doctor
36 1.2898175 0.8927383 0.1742001 0.8337975 0.9516791 0.0660225 mean_queue_length_doctor
37 1.2600902 0.9026667 0.1820713 0.8419611 0.9633723 0.0672514 mean_queue_length_doctor
38 0.9610278 0.9042025 0.1798434 0.8450895 0.9633156 0.0653759 mean_queue_length_doctor
39 0.8588293 0.9030391 0.1776099 0.8454646 0.9606136 0.0637564 mean_queue_length_doctor
40 0.7175814 0.8984027 0.1777535 0.8415544 0.9552510 0.0632771 mean_queue_length_doctor
41 0.8762122 0.8978614 0.1755517 0.8424505 0.9532724 0.0617144 mean_queue_length_doctor
42 1.0504412 0.9014943 0.1749887 0.8469640 0.9560246 0.0604888 mean_queue_length_doctor
43 0.7479977 0.8979246 0.1744703 0.8442306 0.9516186 0.0597979 mean_queue_length_doctor
44 1.0019122 0.9002880 0.1731408 0.8476483 0.9529276 0.0584698 mean_queue_length_doctor
45 0.6953367 0.8957335 0.1738674 0.8434979 0.9479690 0.0583160 mean_queue_length_doctor
46 0.7645500 0.8928817 0.1730093 0.8415043 0.9442591 0.0575411 mean_queue_length_doctor
47 0.9318572 0.8937109 0.1712129 0.8434410 0.9439809 0.0562486 mean_queue_length_doctor
48 1.0725052 0.8974358 0.1713363 0.8476849 0.9471867 0.0554367 mean_queue_length_doctor
49 0.8105346 0.8956623 0.1699961 0.8468338 0.9444909 0.0545167 mean_queue_length_doctor
50 0.8308819 0.8943667 0.1685017 0.8464791 0.9422544 0.0535436 mean_queue_length_doctor 
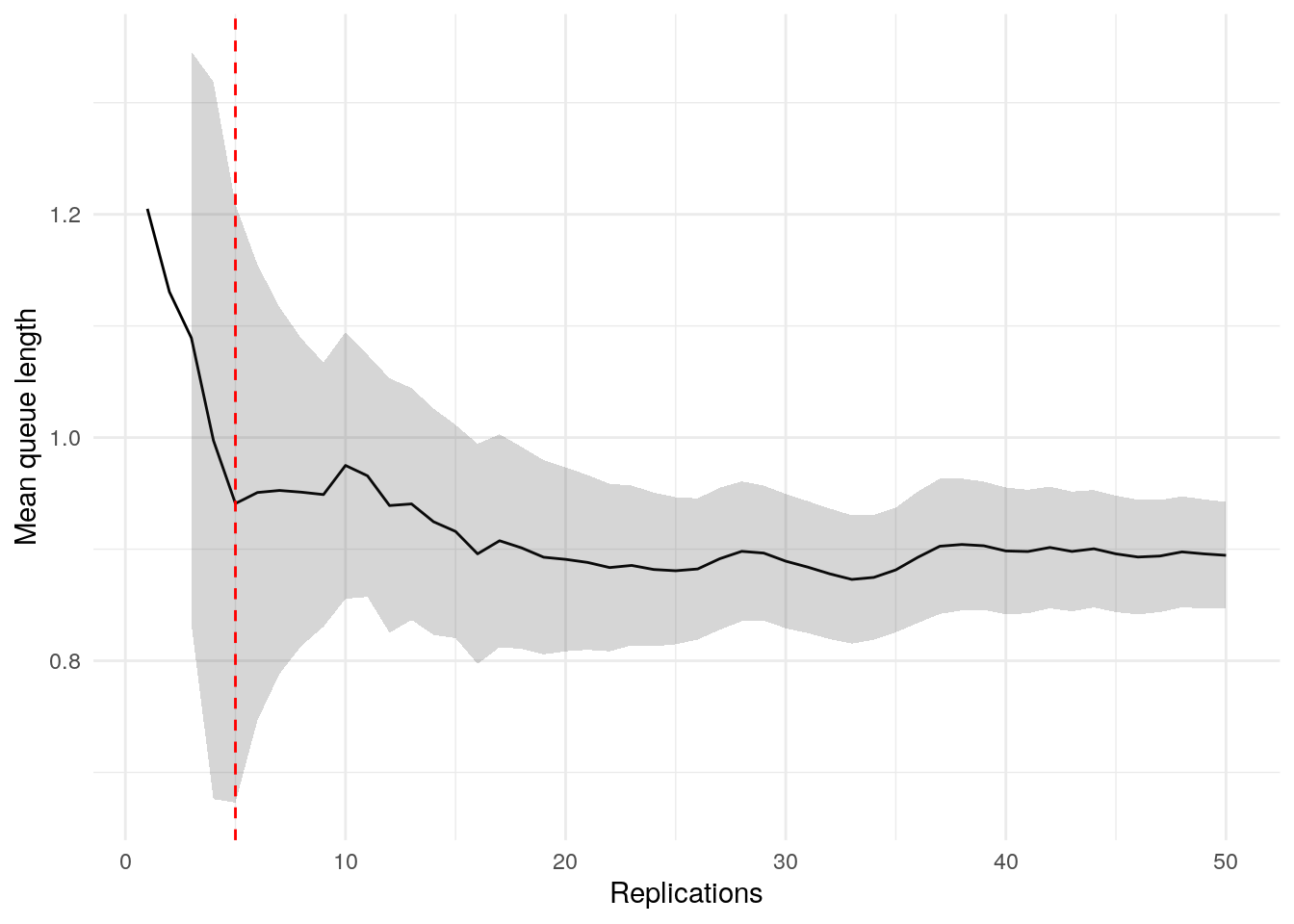
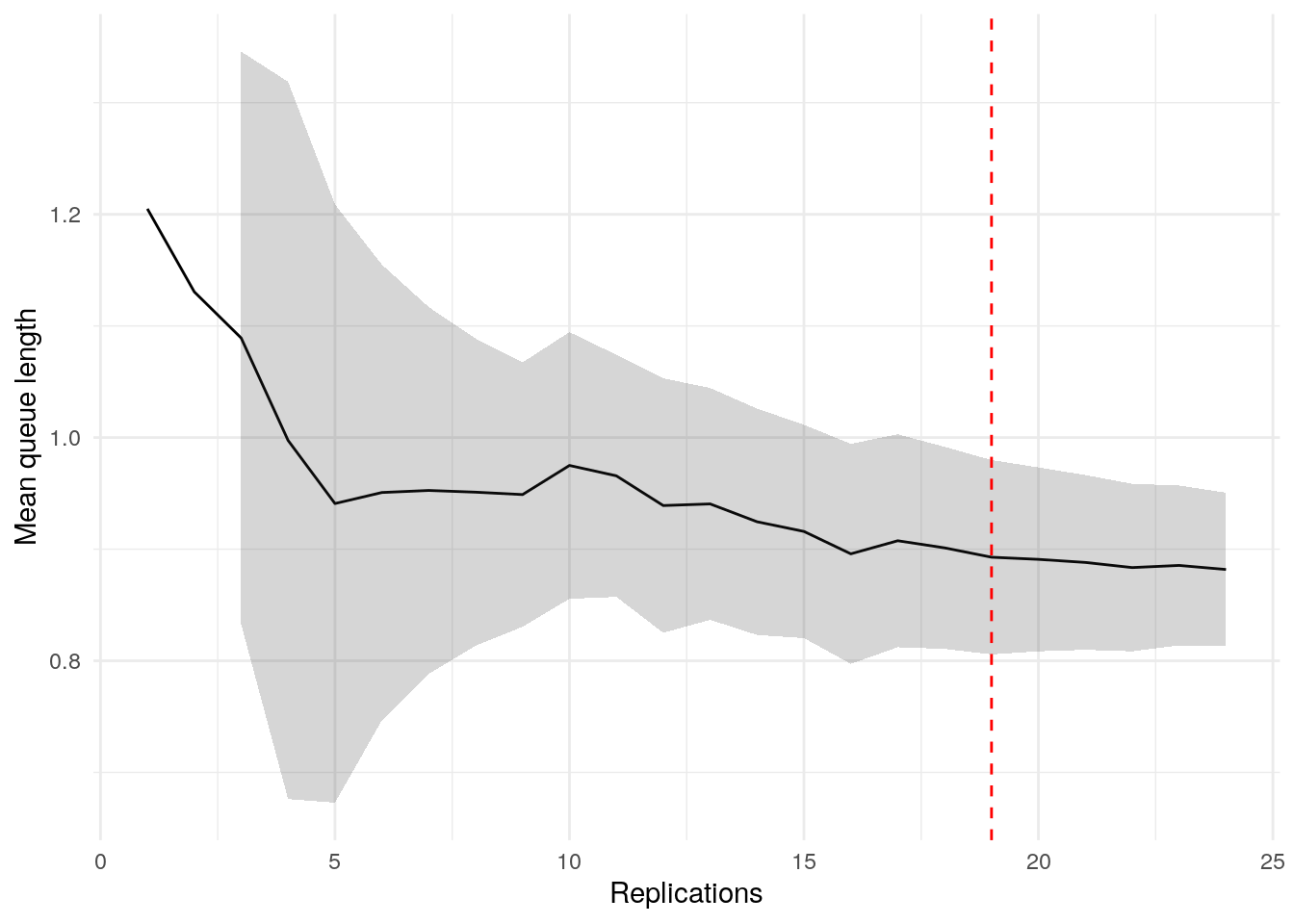
plot_replication_ci(
  conf_ints = ci_df[["mean_queue_length_doctor"]],
  yaxis_title = "Mean queue length",
  min_rep = 5L
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

ci_df[["mean_time_in_system"]] |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 15.58670 15.58670 NA NA NA NA mean_time_in_system
2 15.64705 15.61688 NA NA NA NA mean_time_in_system
3 14.80302 15.34559 0.4708495 14.17594 16.51525 0.0762209 mean_time_in_system
4 13.42023 14.86425 1.0366078 13.21478 16.51372 0.1109692 mean_time_in_system
5 13.41904 14.57521 1.1061844 13.20170 15.94872 0.0942360 mean_time_in_system
6 14.99688 14.64549 1.0042656 13.59157 15.69940 0.0719616 mean_time_in_system
7 15.06660 14.70564 0.9304792 13.84509 15.56619 0.0585183 mean_time_in_system
8 14.92535 14.73311 0.8649513 14.00999 15.45622 0.0490811 mean_time_in_system
9 14.23345 14.67759 0.8260523 14.04263 15.31255 0.0432605 mean_time_in_system
10 16.53909 14.86374 0.9762495 14.16537 15.56211 0.0469846 mean_time_in_system
11 14.02954 14.78790 0.9596977 14.14317 15.43264 0.0435987 mean_time_in_system
12 13.17471 14.65347 1.0267213 14.00112 15.30582 0.0445183 mean_time_in_system
13 14.92982 14.67473 0.9859944 14.07890 15.27056 0.0406025 mean_time_in_system
14 12.87660 14.54629 1.0622377 13.93297 15.15961 0.0421632 mean_time_in_system
15 13.82593 14.49827 1.0403592 13.92214 15.07440 0.0397380 mean_time_in_system
16 12.73663 14.38816 1.0973382 13.80343 14.97290 0.0406397 mean_time_in_system
17 15.39315 14.44728 1.0900934 13.88681 15.00776 0.0387944 mean_time_in_system
18 13.73073 14.40747 1.0709475 13.87490 14.94004 0.0369648 mean_time_in_system
19 13.36509 14.35261 1.0678943 13.83790 14.86732 0.0358617 mean_time_in_system
20 14.33452 14.35171 1.0394199 13.86524 14.83817 0.0338959 mean_time_in_system
21 14.52219 14.35982 1.0137840 13.89836 14.82129 0.0321361 mean_time_in_system
22 13.99784 14.34337 0.9923574 13.90338 14.78336 0.0306753 mean_time_in_system
23 14.60215 14.35462 0.9710418 13.93471 14.77453 0.0292526 mean_time_in_system
24 13.96176 14.33825 0.9530773 13.93580 14.74070 0.0280682 mean_time_in_system
25 13.95520 14.32293 0.9361503 13.93651 14.70935 0.0269794 mean_time_in_system
26 14.74119 14.33902 0.9208968 13.96706 14.71098 0.0259403 mean_time_in_system
27 15.33368 14.37586 0.9230796 14.01070 14.74101 0.0254008 mean_time_in_system
28 15.72428 14.42401 0.9409861 14.05914 14.78889 0.0252964 mean_time_in_system
29 14.09975 14.41283 0.9259899 14.06061 14.76506 0.0244385 mean_time_in_system
30 12.81237 14.35948 0.9556530 14.00264 14.71633 0.0248509 mean_time_in_system
31 13.79822 14.34138 0.9449825 13.99476 14.68800 0.0241694 mean_time_in_system
32 13.06655 14.30154 0.9565421 13.95667 14.64641 0.0241142 mean_time_in_system
33 13.54228 14.27853 0.9507098 13.94143 14.61564 0.0236094 mean_time_in_system
34 14.06356 14.27221 0.9369199 13.94530 14.59912 0.0229051 mean_time_in_system
35 15.32178 14.30220 0.9399334 13.97932 14.62508 0.0225754 mean_time_in_system
36 16.33737 14.35873 0.9865529 14.02493 14.69253 0.0232473 mean_time_in_system
37 16.33898 14.41225 1.0257850 14.07024 14.75426 0.0237308 mean_time_in_system
38 14.24194 14.40777 1.0122052 14.07507 14.74047 0.0230920 mean_time_in_system
39 14.38384 14.40715 0.9988053 14.08338 14.73093 0.0224732 mean_time_in_system
40 13.33151 14.38026 1.0004786 14.06030 14.70023 0.0222505 mean_time_in_system
41 14.17813 14.37533 0.9883977 14.06336 14.68731 0.0217022 mean_time_in_system
42 15.37684 14.39918 0.9884250 14.09116 14.70719 0.0213911 mean_time_in_system
43 13.58958 14.38035 0.9843604 14.07741 14.68329 0.0210663 mean_time_in_system
44 14.75626 14.38889 0.9744962 14.09262 14.68517 0.0205905 mean_time_in_system
45 13.11879 14.36067 0.9817882 14.06571 14.65563 0.0205396 mean_time_in_system
46 13.63696 14.34494 0.9766647 14.05490 14.63497 0.0202185 mean_time_in_system
47 14.18810 14.34160 0.9662613 14.05790 14.62531 0.0197820 mean_time_in_system
48 15.78832 14.37174 0.9784682 14.08762 14.65586 0.0197692 mean_time_in_system
49 13.49178 14.35378 0.9763488 14.07334 14.63422 0.0195377 mean_time_in_system
50 13.85929 14.34389 0.9688618 14.06854 14.61924 0.0191961 mean_time_in_system 
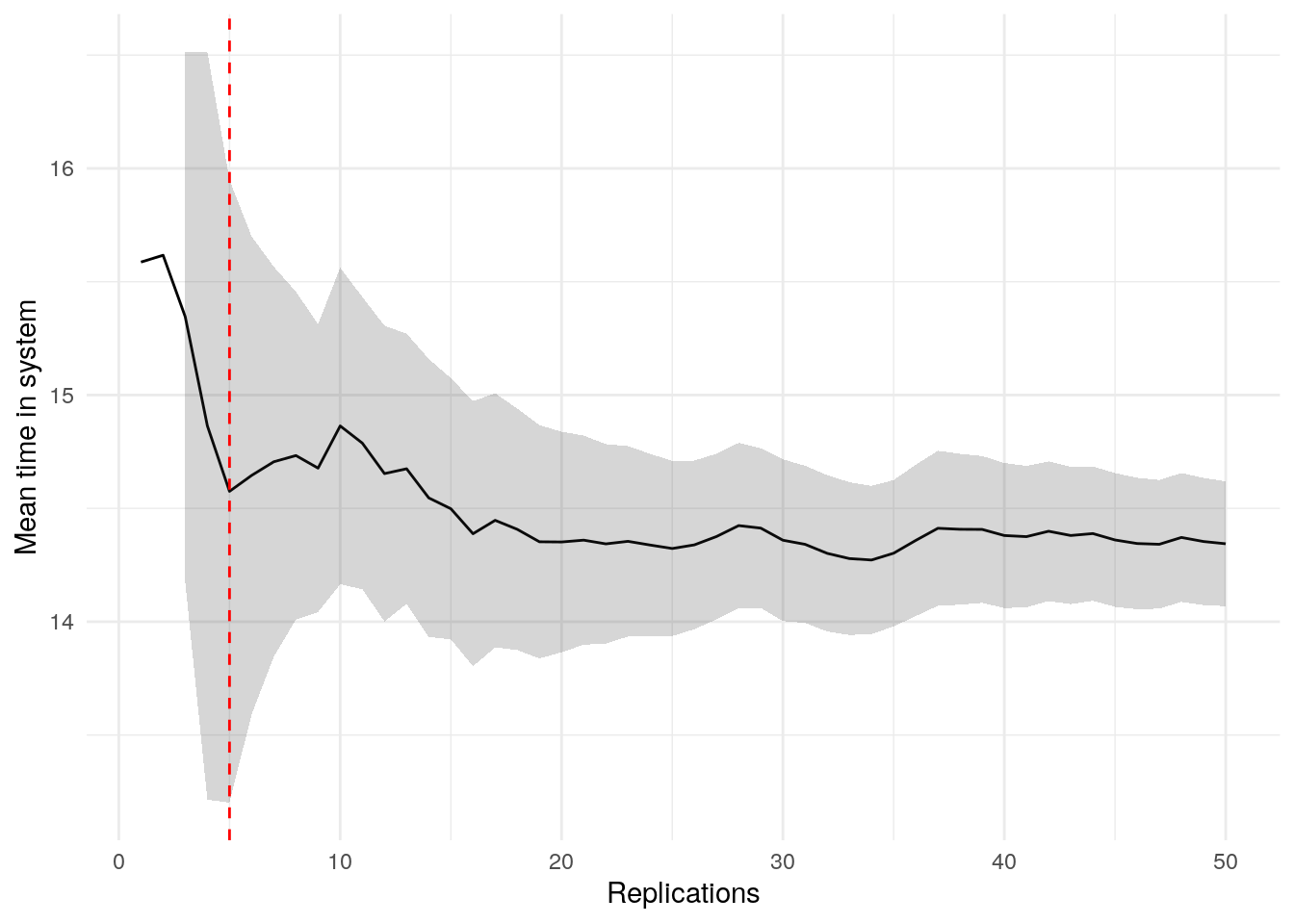
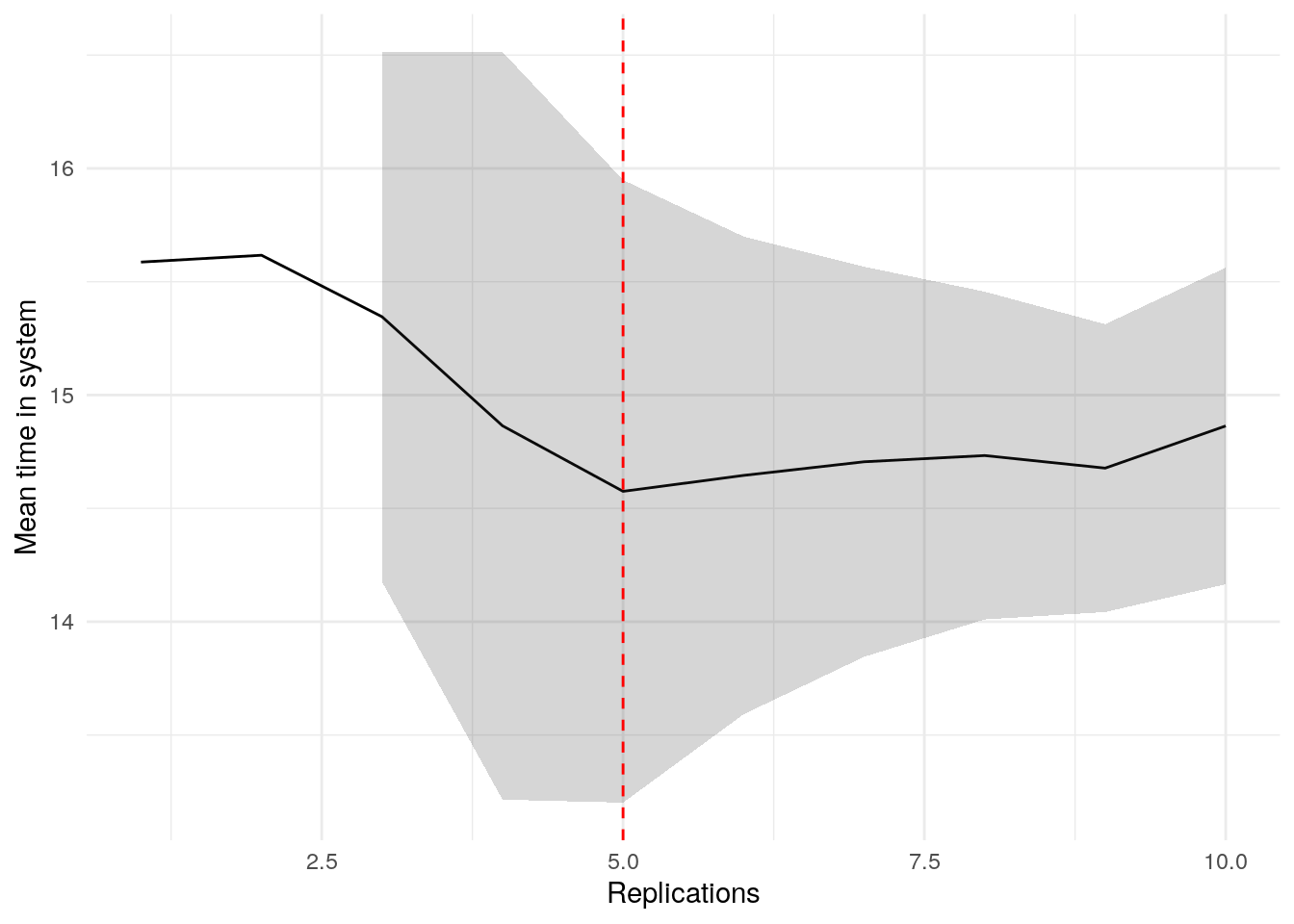
plot_replication_ci(
  conf_ints = ci_df[["mean_time_in_system"]],
  yaxis_title = "Mean time in system",
  min_rep = 5L
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

ci_df[["mean_patients_in_system"]] |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 3.220799 3.220799 NA NA NA NA mean_patients_in_system
2 3.200296 3.210548 NA NA NA NA mean_patients_in_system
3 2.910529 3.110542 0.1735187 2.679497 3.541586 0.1385753 mean_patients_in_system
4 2.658131 2.997439 0.2669107 2.572724 3.422153 0.1416925 mean_patients_in_system
5 2.727798 2.943511 0.2607148 2.619791 3.267231 0.1099776 mean_patients_in_system
6 3.039950 2.959584 0.2364907 2.711402 3.207766 0.0838570 mean_patients_in_system
7 2.992402 2.964272 0.2162415 2.764282 3.164262 0.0674668 mean_patients_in_system
8 2.906402 2.957038 0.2012436 2.788795 3.125282 0.0568961 mean_patients_in_system
9 2.914509 2.952313 0.1887791 2.807205 3.097421 0.0491508 mean_patients_in_system
10 3.267347 2.983816 0.2039668 2.837907 3.129726 0.0489002 mean_patients_in_system
11 2.794186 2.966577 0.2017704 2.831026 3.102128 0.0456928 mean_patients_in_system
12 2.564186 2.933045 0.2247298 2.790258 3.075831 0.0486820 mean_patients_in_system
13 2.891613 2.929858 0.2154690 2.799651 3.060064 0.0444413 mean_patients_in_system
14 2.583487 2.905117 0.2267710 2.774183 3.036050 0.0450700 mean_patients_in_system
15 2.774866 2.896434 0.2210947 2.773995 3.018872 0.0422721 mean_patients_in_system
16 2.467407 2.869619 0.2390146 2.742257 2.996981 0.0443829 mean_patients_in_system
17 3.140526 2.885555 0.2405714 2.761865 3.009245 0.0428654 mean_patients_in_system
18 2.794623 2.880503 0.2343706 2.763953 2.997053 0.0404616 mean_patients_in_system
19 2.600749 2.865779 0.2366368 2.751724 2.979835 0.0397991 mean_patients_in_system
20 2.888899 2.866935 0.2303834 2.759113 2.974758 0.0376091 mean_patients_in_system
21 2.855192 2.866376 0.2245646 2.764156 2.968597 0.0356620 mean_patients_in_system
22 2.798657 2.863298 0.2196276 2.765921 2.960675 0.0340088 mean_patients_in_system
23 2.987137 2.868682 0.2161262 2.775222 2.962142 0.0325794 mean_patients_in_system
24 2.777398 2.864879 0.2121953 2.775276 2.954481 0.0312761 mean_patients_in_system
25 2.776448 2.861341 0.2084790 2.775286 2.947397 0.0300754 mean_patients_in_system
26 2.888231 2.862376 0.2043350 2.779843 2.944908 0.0288336 mean_patients_in_system
27 3.100114 2.871181 0.2055243 2.789878 2.952484 0.0283168 mean_patients_in_system
28 3.144160 2.880930 0.2081757 2.800208 2.961652 0.0280195 mean_patients_in_system
29 2.774958 2.877276 0.2053694 2.799158 2.955394 0.0271501 mean_patients_in_system
30 2.682587 2.870786 0.2049041 2.794274 2.947299 0.0266521 mean_patients_in_system
31 2.574375 2.861225 0.2083755 2.784792 2.937657 0.0267133 mean_patients_in_system
32 2.646656 2.854519 0.2084669 2.779359 2.929680 0.0263303 mean_patients_in_system
33 2.708765 2.850103 0.2067465 2.776794 2.923412 0.0257216 mean_patients_in_system
34 2.921153 2.852192 0.2039542 2.781029 2.923355 0.0249503 mean_patients_in_system
35 3.168527 2.861230 0.2079253 2.789806 2.932655 0.0249630 mean_patients_in_system
36 3.287012 2.873058 0.2168722 2.799679 2.946437 0.0255404 mean_patients_in_system
37 3.296415 2.884500 0.2248803 2.809521 2.959479 0.0259937 mean_patients_in_system
38 2.853276 2.883678 0.2218783 2.810748 2.956608 0.0252905 mean_patients_in_system
39 2.883394 2.883671 0.2189394 2.812699 2.954643 0.0246117 mean_patients_in_system
40 2.762898 2.880651 0.2169563 2.811266 2.950038 0.0240869 mean_patients_in_system
41 2.835098 2.879540 0.2143453 2.811885 2.947196 0.0234953 mean_patients_in_system
42 3.103644 2.884876 0.2145206 2.818027 2.951726 0.0231723 mean_patients_in_system
43 2.682198 2.880163 0.2141932 2.814244 2.946082 0.0228872 mean_patients_in_system
44 2.970183 2.882209 0.2121225 2.817718 2.946700 0.0223756 mean_patients_in_system
45 2.610948 2.876181 0.2135614 2.812020 2.940342 0.0223077 mean_patients_in_system
46 2.739242 2.873204 0.2121382 2.810207 2.936201 0.0219258 mean_patients_in_system
47 2.849724 2.872704 0.2098476 2.811091 2.934318 0.0214479 mean_patients_in_system
48 3.150293 2.878487 0.2114342 2.817093 2.939881 0.0213286 mean_patients_in_system
49 2.797787 2.876840 0.2095375 2.816654 2.937027 0.0209209 mean_patients_in_system
50 2.864371 2.876591 0.2073959 2.817650 2.935532 0.0204900 mean_patients_in_system 
plot_replication_ci(
  conf_ints = ci_df[["mean_patients_in_system"]],
  yaxis_title = "Mean number of patients in system",
  min_rep = 5L
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

Automated

Description of the algorithm

Using the automated method, an algorithm will tell us the number of runs needed. We will use the ReplicationsAlgorithm class from sim-tools.

Here’s how it works:

  • The algorithm runs the simulation model repeatedly, for an increasing number of runs.
  • After each run, it checks if the results are stable enough. It does this by looking at the percentage deviation of the confidence interval from the mean.
  • The algorithm also incorporates a look-ahead period, meaning it continues to run the simulation and check that results stay stable for the next few runs (and that this wasn’t just a lucky one-off!).

Model adapter

The ReplicationsAlgorithm can be used on a variety of model structures - it just requires a standardised interface, as defined by the ReplicationsAlgorithmModelAdapter class in sim-tools

What this essentially tells us is that the model needs to provide a single_run(replication_number) method, returning results in dictionary form.

@runtime_checkable
class ReplicationsAlgorithmModelAdapter(Protocol):
    """
    Adapter pattern for the "Replications Algorithm".

    All models that use ReplicationsAlgorithm must provide a
    single_run(replication_number) interface.
    """

    def single_run(self, replication_number: int) -> dict[str, float]:
        """
        Run a single unique replication of the model and return results.

        Parameters
        ----------
        replication_number : int
            The replication sequence number.

        Returns
        -------
        dict[str, float]
            {'metric_name': value, ... } for all metrics being tracked.
        """


To achieve this, we wrap our model’s own execution logic inside an adapter class. The SimulationAdapter encapsulates simulation parameters, a runner, and the list of metrics you want to extract. Each call to single_run executes one replication and returns results in the correct dictionary format.

class SimulationAdapter:
    """
    Adapter for running model replications compatible with
    ReplicationsAlgorithm.

    Attributes
    ----------
    param : Parameters
        The simulation parameter object for Runner.
    metrics : list[str]
        The metric(s) to output from each run.
    runner : Runner
        An instance of runner initialised with the provided parameters.
    """
    def __init__(self, param, metrics):
        """
        Initialise adapter.

        Parameters
        ----------
        param : Parameters
            The simulation parameter object for Runner.
        metrics : list[str]
            The metric(s) to output from each run.
        """
        self.param = param
        self.metrics = metrics
        self.runner = Runner(self.param)

    def single_run(self, replication_number):
        """
        Run a single simulation replication and return required metrics.
        """
        result = self.runner.run_single(run=replication_number)
        return {metric: result["run"][metric] for metric in self.metrics}


For example:

adapter = SimulationAdapter(param=Parameters(), metrics=metrics)
adapter.single_run(replication_number=0)
{'mean_wait_time': np.float64(3.227077467801481), 'mean_utilisation_tw': 0.8743911437929205, 'mean_queue_length': 0.6102042855882626, 'mean_time_in_system': np.float64(15.849646506571181), 'mean_patients_in_system': 3.2333777169670244}

Run algorithm

We can then use this adapter to run ReplicationsAlgorithm.

# Set up model with adapter
sim_model = SimulationAdapter(
  param=Parameters(warm_up_period=10000,
                   data_collection_period=10000),
  metrics=metrics)

# Set up and run the algorithm
analyser = ReplicationsAlgorithm(
    alpha=0.05,
    half_width_precision=0.1,
    look_ahead=5,
    replication_budget=100,
    verbose=False
)
nreps, summary_frame = analyser.select(model=sim_model, metrics=metrics)


The algorithm returns:

  1. The number of replications required for each metric (here, assigned to nreps).
  2. A dataframe containing the cumulative results and deviations for each metric (in a single dataframe, here assigned to summary_frame).
# View results
print(nreps)
{'mean_wait_time': 24, 'mean_utilisation_tw': 3, 'mean_queue_length': 24, 'mean_time_in_system': 9, 'mean_patients_in_system': 9}
HTML(to_html_datatable(summary_frame))
Loading ITables v2.5.2 from the internet... (need help?)


Again, we can use plotly_confidence_interval_method to create plots.

p = plotly_confidence_interval_method(
    n_reps=nreps["mean_wait_time"],
    conf_ints=summary_frame[
        summary_frame["metric"] == "mean_wait_time"].reset_index(),
    metric_name="Mean Wait Time")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=nreps["mean_utilisation_tw"],
    conf_ints=summary_frame[
        summary_frame["metric"] == "mean_utilisation_tw"].reset_index(),
    metric_name="Mean Utilisation")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=nreps["mean_queue_length"],
    conf_ints=summary_frame[
        summary_frame["metric"] == "mean_queue_length"].reset_index(),
    metric_name="Mean Queue Length")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=nreps["mean_time_in_system"],
    conf_ints=summary_frame[
        summary_frame["metric"] == "mean_time_in_system"].reset_index(),
    metric_name="Mean Time In System")
p.update_layout(autosize=True, width=None, height=390)
p = plotly_confidence_interval_method(
    n_reps=nreps["mean_patients_in_system"],
    conf_ints=summary_frame[
        summary_frame["metric"] == "mean_patients_in_system"].reset_index(),
    metric_name="Mean Patients In System")
p.update_layout(autosize=True, width=None, height=390)

For this analysis, we have created three R6 classes: WelfordStats, ReplicationTabuliser, and ReplicationsAlgorithm.

#' Computes running sample mean and variance using Welford's algorithm.
#'
#' @description
#' They are computed via updates to a stored value, rather than storing lots of
#' data and repeatedly taking the mean after new values have been added.
#'
#' Implements Welford's algorithm for updating mean and variance.
#' See Knuth. D `The Art of Computer Programming` Vol 2. 2nd ed. Page 216.
#'
#' This class is based on the Python class `OnlineStatistics` from Tom Monks
#' (2021) sim-tools: fundamental tools to support the simulation process in
#' python (https://github.com/TomMonks/sim-tools) (MIT Licence).
#'
#' @docType class
#' @importFrom R6 R6Class
#'
#' @return Object of `R6Class` with methods for running mean and variance
#' calculation.
#' @export

WelfordStats <- R6Class("WelfordStats", list( # nolint: object_name_linter

  #' @field n Number of observations.
  n = 0L,

  #' @field latest_data Latest data point.
  latest_data = NA,

  #' @field mean Running mean.
  mean = NA,

  #' @field sq Running sum of squares of differences.
  sq = NA,

  #' @field alpha Significance level for confidence interval calculations.
  #' For example, if alpha is 0.05, then the confidence level is 95\%.
  alpha = NA,

  #' @field observer Observer to notify on updates.
  observer = NULL,

  #' @description Initialise the WelfordStats object.
  #' @param data Initial data sample.
  #' @param alpha Significance level for confidence interval calculations.
  #' @param observer Observer to notify on updates.
  #' @return A new `WelfordStats` object.
  initialize = function(data = NULL, alpha = 0.05, observer = NULL) {
    # Set alpha and observer using the provided values/objects
    self$alpha <- alpha
    self$observer <- observer
    # If an initial data sample is supplied, then run update()
    if (!is.null(data)) {
      for (x in as.matrix(data)) {
        self$update(x)
      }
    }
  },

  #' @description Update running statistics with a new data point.
  #' @param x A new data point.
  update = function(x) {
    # Increment counter and save the latest data point
    self$n <- self$n + 1L
    self$latest_data <- x
    # Calculate the mean and sq
    if (self$n == 1L) {
      self$mean <- x
      self$sq <- 0L
    } else {
      updated_mean <- self$mean + ((x - self$mean) / self$n)
      self$sq <- self$sq + ((x - self$mean) * (x - updated_mean))
      self$mean <- updated_mean
    }
    # Update observer if present
    if (!is.null(self$observer)) {
      self$observer$update(self)
    }
  },

  #' @description Computes the variance of the data points.
  variance = function() {
    self$sq / (self$n - 1L)
  },

  #' @description Computes the standard deviation.
  std = function() {
    if (self$n < 3L) return(NA_real_)
    sqrt(self$variance())
  },

  #' @description Computes the standard error of the mean.
  std_error = function() {
    self$std() / sqrt(self$n)
  },

  #' @description Computes the half-width of the confidence interval.
  half_width = function() {
    if (self$n < 3L) return(NA_real_)
    dof <- self$n - 1L
    t_value <- qt(1L - (self$alpha / 2L), df = dof)
    t_value * self$std_error()
  },

  #' @description Computes the lower confidence interval bound.
  lci = function() {
    self$mean - self$half_width()
  },

  #' @description Computes the upper confidence interval bound.
  uci = function() {
    self$mean + self$half_width()
  },

  #' @description Computes the precision of the confidence interval expressed
  #' as the percentage deviation of the half width from the mean.
  deviation = function() {
    mw <- self$mean
    if (is.na(mw) || mw == 0L) return(NA_real_)
    self$half_width() / mw
  }
))
#' Observes and records results from WelfordStats.
#'
#' @description
#' Updates each time new data is processed. Can generate a results dataframe.
#'
#' This class is based on the Python class `ReplicationTabulizer` from Tom
#' Monks (2021) sim-tools: fundamental tools to support the simulation process
#' in python (https://github.com/TomMonks/sim-tools) (MIT Licence).
#'
#' @docType class
#' @importFrom R6 R6Class
#'
#' @return Object of `R6Class` with methods for storing and tabulising results.
#' @export

ReplicationTabuliser <- R6Class("ReplicationTabuliser", list( # nolint: object_name_linter

  #' @field data_points List containing each data point.
  data_points = NULL,

  #' @field cumulative_mean List of the running mean.
  cumulative_mean = NULL,

  #' @field std List of the standard deviation.
  std = NULL,

  #' @field lci List of the lower confidence interval bound.
  lci = NULL,

  #' @field uci List of the upper confidence interval bound.
  uci = NULL,

  #' @field deviation List of the percentage deviation of the confidence
  #' interval half width from the mean.
  deviation = NULL,

  #' @description Add new results from WelfordStats to the appropriate lists.
  #' @param stats An instance of WelfordStats containing updated statistical
  #' measures like the mean, standard deviation and confidence intervals.
  update = function(stats) {
    self$data_points <- c(self$data_points, stats$latest_data)
    self$cumulative_mean <- c(self$cumulative_mean, stats$mean)
    self$std <- c(self$std, stats$std())
    self$lci <- c(self$lci, stats$lci())
    self$uci <- c(self$uci, stats$uci())
    self$deviation <- c(self$deviation, stats$deviation())
  },

  #' @description Creates a results table from the stored lists.
  #' @return Stored results compiled into a dataframe.
  summary_table = function() {
    data.frame(
      replications = seq_len(length(self$data_points)),
      data = self$data_points,
      cumulative_mean = self$cumulative_mean,
      stdev = self$std,
      lower_ci = self$lci,
      upper_ci = self$uci,
      deviation = self$deviation
    )
  }
))
#' Replication algorithm to automatically select number of replications.
#'
#' @description
#' Implements an adaptive replication algorithm for selecting the
#' appropriate number of simulation replications based on statistical
#' precision.
#'
#' Uses the "Replications Algorithm" from Hoad, Robinson, & Davies (2010).
#' Automated selection of the number of replications for a discrete-event
#' simulation. Journal of the Operational Research Society.
#' https://www.jstor.org/stable/40926090.
#'
#' Given a model's performance measure and a user-set confidence interval
#' half width prevision, automatically select the number of replications.
#' Combines the "confidence intervals" method with a sequential look-ahead
#' procedure to determine if a desired precision in the confidence interval
#' is maintained.
#'
#' This class is based on the Python class `ReplicationsAlgorithm` from Tom
#' Monks (2021) sim-tools: fundamental tools to support the simulation process
#' in python (https://github.com/TomMonks/sim-tools) (MIT Licence).
#'
#' @docType class
#' @importFrom R6 R6Class
#'
#' @return Object of `ReplicationsAlgorithm` with methods for determining the
#' appropriate number of replications to use.
#' @export

ReplicationsAlgorithm <- R6Class("ReplicationsAlgorithm", list( # nolint: object_name_linter

  #' @field param Model parameters.
  param = NA,

  #' @field metrics List of performance measure to track (should correspond to
  #' column names from the run results dataframe).
  metrics  = NA,

  #' @field desired_precision The target half width precision for the algorithm
  #' (i.e. percentage deviation of the confidence interval from the mean,
  #' expressed as a proportion, e.g. 0.1 = 10\%). Choice is fairly arbitrary.
  desired_precision = NA,

  #' @field initial_replications Number of initial replications to perform.
  initial_replications = NA,

  #' @field look_ahead Minimum additional replications to look ahead to assess
  #' stability of precision. When the number of replications is <= 100, the
  #' value of look_ahead is used. When they are > 100, then
  #' look_ahead / 100 * max(n, 100) is used.
  look_ahead = NA,

  #' @field replication_budget Maximum allowed replications. Use for larger
  #' models where replication runtime is a constraint.
  replication_budget = NA,

  #' @field reps Number of replications performed.
  reps = NA,

  #' @field nreps The minimum number of replicatons required to achieve
  #' desired precision for each metric.
  nreps = NA,

  #' @field summary_table Dataframe containing cumulative statistics for each
  #' replication for each metric
  summary_table = NA,

  #' @description Initialise the ReplicationsAlgorithm object.
  #' @param param Model parameters.
  #' @param metrics List of performance measure to track.
  #' @param desired_precision Target half width precision for the algorithm.
  #' @param initial_replications Number of initial replications to perform.
  #' @param look_ahead Minimum additional replications to look ahead.
  #' @param replication_budget Maximum allowed replications.
  #' @param verbose Boolean, whether to print messages about parameters.
  initialize = function(
    param,
    metrics,
    desired_precision = 0.1,
    initial_replications = 3L,
    look_ahead = 5L,
    replication_budget = 1000L,
    verbose = TRUE
  ) {
    self$param <- param
    self$metrics <- metrics
    self$desired_precision <- desired_precision
    self$initial_replications <- initial_replications
    self$look_ahead <- look_ahead
    self$replication_budget <- replication_budget

    # Initially set reps to the number of initial replications
    self$reps <- initial_replications

    # Print the parameters
    if (isTRUE(verbose)) {
      print("Model parameters:")  # nolint: print_linter
      print(self$param)
    }

    # Check validity of provided parameters
    self$valid_inputs()
  },

  #' @description
  #' Checks validity of provided parameters.
  valid_inputs = function() {
    for (p in c("initial_replications", "look_ahead")) {
      if (self[[p]] %% 1L != 0L || self[[p]] < 0L) {
        stop(p, " must be a non-negative integer, but provided ", self[[p]],
             ".", call. = FALSE)
      }
    }
    if (self$desired_precision <= 0L) {
      stop("desired_precision must be greater than 0.", call. = FALSE)
    }
    if (self$replication_budget < self$initial_replications) {
      stop("replication_budget must be less than initial_replications.",
           call. = FALSE)
    }
  },

  #' @description
  #' Calculate the klimit. Determines the number of additional replications to
  #' check after precision is reached, scaling with total replications if they
  #' are greater than 100. Rounded down to nearest integer.
  #' @return Number of additional replications to verify stability (integer).
  klimit = function() {
    as.integer((self$look_ahead / 100L) * max(self$reps, 100L))
  },

  #' @description
  #' Find the first position where element is below deviation, and this is
  #' maintained through the lookahead period.
  #' This is used to correct the ReplicationsAlgorithm, which cannot return
  #' a solution below the initial_replications.
  #' @param lst List of numbers to compare against desired deviation.
  #' @return Integer, minimum replications required to meet and maintain
  #' precision.
  find_position = function(lst) {
    # Ensure that the input is a list
    if (!is.list(lst)) {
      stop("find_position requires a list but was supplied: ", typeof(lst),
           call. = FALSE)
    }

    # Check if list is empty or no values below threshold
    if (length(lst) == 0L || all(is.na(lst)) || !any(unlist(lst) < 0.5)) {
      return(NULL)
    }

    # Find the first non-null value in the list
    start_index <- which(!vapply(lst, is.na, logical(1L)))[1L]

    # Iterate through the list, stopping when at last point where we still
    # have enough elements to look ahead
    max_index <- length(lst) - self$look_ahead
    if (start_index > max_index) {
      return(NULL)
    }
    for (i in start_index:max_index) {
      # Trim to list with current value + lookahead
      # Check if all fall below the desired deviation
      segment <- lst[i:(i + self$look_ahead)]
      if (all(vapply(segment,
                     function(x) x < self$desired_precision, logical(1L)))) {
        return(i)
      }
    }
    return(NULL) # nolint: return_linter
  },

  #' @description
  #' Executes the replication algorithm, determining the necessary number
  #' of replications to achieve and maintain the desired precision.
  select = function() {

    # Create instances of observers for each metric
    observers <- setNames(
      lapply(self$metrics, function(x) ReplicationTabuliser$new()), self$metrics
    )

    # Create nested named list to store record for each metric of:
    # - nreps (the solution - replications required for precision)
    # - target_met (record of how many times in a row the target has been meet,
    # used to check if lookahead period has passed)
    # - solved (whether it has maintained precision for lookahead)
    solutions <- setNames(
      lapply(self$metrics, function(x) {
        list(nreps = NA, target_met = 0L, solved = FALSE)
      }), self$metrics
    )

    # If there are no initial replications, create empty instances of
    # WelfordStats for each metric...
    if (self$initial_replications == 0L) {
      stats <- setNames(
        lapply(
          self$metrics, function(x) WelfordStats$new(observer = observers[[x]])
        ), self$metrics
      )
    } else {
      # If there are, run the replications, then create instances of
      # WelfordStats pre-loaded with data from the initial replications... we
      # use runner so allows for parallel processing if desired...
      self$param[["number_of_runs"]] <- self$initial_replications
      result <- runner(self$param)[["run_results"]]
      stats <- setNames(
        lapply(self$metrics, function(x) {
          WelfordStats$new(data = result[[x]], observer = observers[[x]])
        }), self$metrics
      )
      # After completing any replications, check if any have met precision, add
      # solution and update count
      for (metric in self$metrics) {
        if (isTRUE(stats[[metric]]$deviation() < self$desired_precision)) {
          solutions[[metric]]$nreps <- self$reps
          solutions[[metric]]$target_met <- 1L
          # If there is no lookahead, mark as solved
          if (self$klimit() == 0L) {
            solutions[[metric]]$solved <- TRUE
          }
        }
      }
    }

    # Whilst have not yet got all metrics marked as solved = TRUE, and still
    # under replication budget + lookahead...
    is_all_solved <- function(solutions_list) {
      statuses <- unlist(lapply(solutions_list, function(x) x$solved))
      # If any are NA or FALSE, treat as not solved
      all(statuses)
    }

    while (!is_all_solved(solutions) &&
             self$reps < self$replication_budget + self$klimit()) {

      # Increment counter
      self$reps <- self$reps + 1L

      # Run another replication
      result <- model(run_number = self$reps,
                      param = self$param)[["run_results"]]

      # Loop through the metrics...
      for (metric in self$metrics) {

        # If it is not yet solved...
        if (!solutions[[metric]]$solved) {

          # Update the running statistics for that metric
          stats[[metric]]$update(result[[metric]])

          # If precision has been achieved...
          if (isTRUE(stats[[metric]]$deviation() < self$desired_precision)) {

            # Check if target met the time prior - if not, record the solution
            if (solutions[[metric]]$target_met == 0L) {
              solutions[[metric]]$nreps <- self$reps
            }

            # Update how many times precision has been met in a row
            solutions[[metric]]$target_met <- (
              solutions[[metric]]$target_met + 1L
            )

            # Mark as solved if have finished lookahead period
            if (solutions[[metric]]$target_met > self$klimit()) {
              solutions[[metric]]$solved <- TRUE
            }

          } else {
            # If precision was not achieved, ensure nreps is None (e.g. in cases
            # where precision is lost after a success)
            solutions[[metric]]$nreps <- NA
            solutions[[metric]]$target_met <- 0L
          }

        }
      }
    }

    # Correction to result...
    for (metric in names(solutions)){
      # Use find_position() to check for solution in initial replications
      adj_nreps <- self$find_position(as.list(observers[[metric]]$deviation))
      # If there was a maintained solution, replace in solutions
      if (!is.null(adj_nreps) && !is.na(solutions[[metric]]$nreps)) {
        solutions[[metric]]$nreps <- adj_nreps
      }
    }

    # Extract minimum replications for each metric
    self$nreps <- lapply(solutions, function(x) x$nreps)

    # Extract any metrics that were not solved and return warning
    if (anyNA(self$nreps)) {
      unsolved <- names(self$nreps)[vapply(self$nreps, is.na, logical(1L))]
      warning(
        "The replications did not reach the desired precision ",
        "for the following metrics - ", toString(unsolved),
        call. = FALSE
      )
    }

    # Combine observer summary frames into a single table
    summary_tables <- lapply(names(observers), function(name) {
      tab <- observers[[name]]$summary_table()
      tab$metric <- name
      tab
    })
    self$summary_table <- do.call(rbind, summary_tables)
  }
))
# Set up algorithm
alg <- ReplicationsAlgorithm$new(
  param = create_params(warm_up_period = 10000L,
                        data_collection_period = 10000L),
  metrics = metrics
)
[1] "Model parameters:"
$interarrival_time
[1] 5

$consultation_time
[1] 10

$number_of_doctors
[1] 3

$warm_up_period
[1] 10000

$data_collection_period
[1] 10000

$number_of_runs
[1] 5

$verbose
[1] FALSE
# Run algorithm
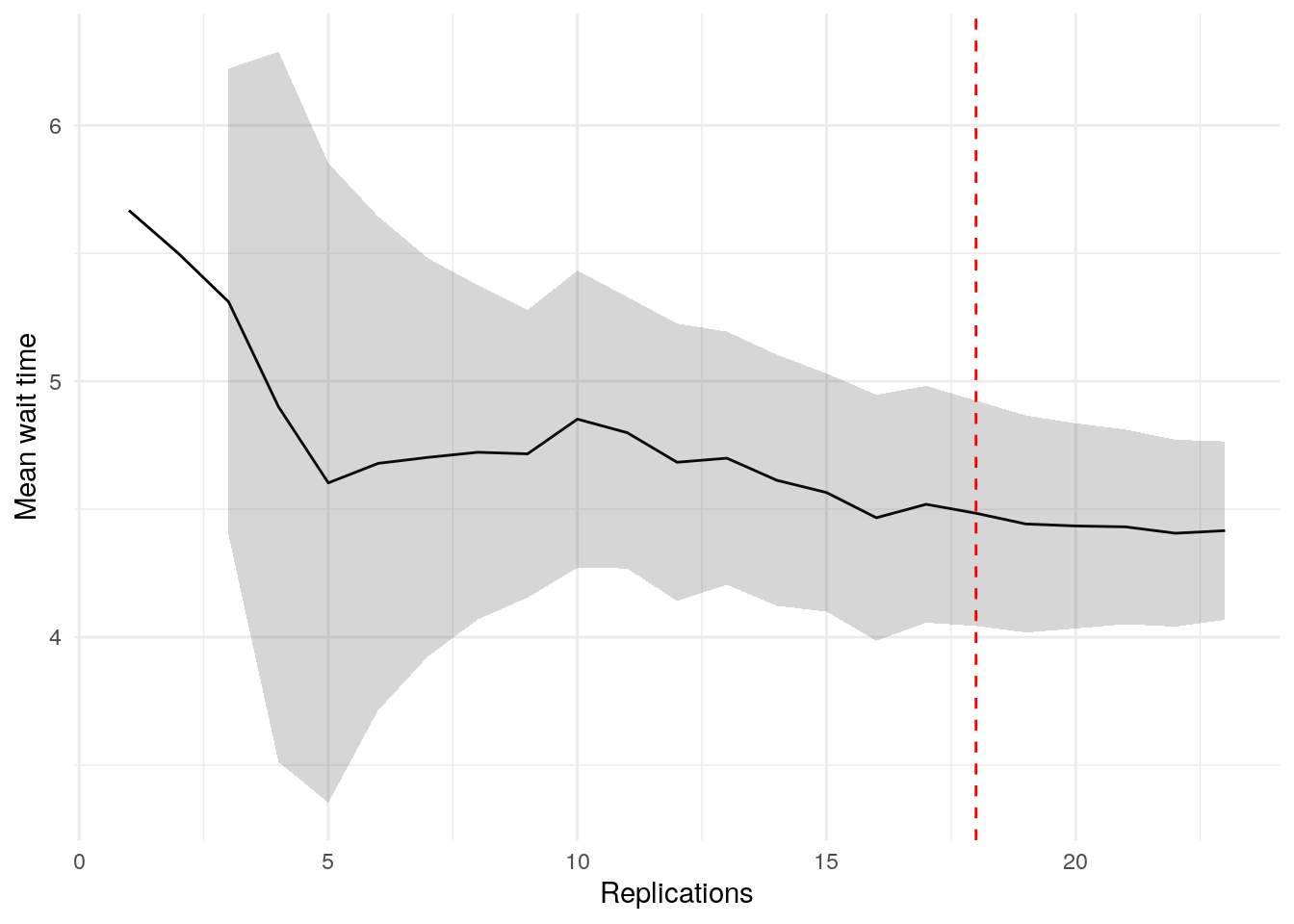
alg$select()

# View recommended number of replications
alg$nreps
$mean_wait_time_doctor
[1] 18

$utilisation_doctor
[1] 3

$mean_queue_length_doctor
[1] 19

$mean_time_in_system
[1] 5

$mean_patients_in_system
[1] 6
# View full results table
alg$summary_table |>
  kable() |>
  scroll_box(height = "400px")
replications data cumulative_mean stdev lower_ci upper_ci deviation metric
1 5.6676719 5.6676719 NA NA NA NA mean_wait_time_doctor
2 5.3283685 5.4980202 NA NA NA NA mean_wait_time_doctor
3 4.9340038 5.3100147 0.3671783 4.3978934 6.2221361 0.1717738 mean_wait_time_doctor
4 3.6718311 4.9004688 0.8722335 3.5125507 6.2883870 0.2832215 mean_wait_time_doctor
5 3.4128133 4.6029377 1.0065869 3.3530950 5.8527805 0.2715315 mean_wait_time_doctor
6 5.0599633 4.6791087 0.9194487 3.7142064 5.6440109 0.2062150 mean_wait_time_doctor
7 4.8427498 4.7024860 0.8416138 3.9241231 5.4808489 0.1655216 mean_wait_time_doctor
8 4.8621394 4.7224426 0.7812248 4.0693224 5.3755629 0.1383014 mean_wait_time_doctor
9 4.6672848 4.7163140 0.7310001 4.1544175 5.2782104 0.1191389 mean_wait_time_doctor
10 6.0724262 4.8519252 0.8117215 4.2712546 5.4325958 0.1196784 mean_wait_time_doctor
11 4.2691492 4.7989456 0.7898594 4.2683108 5.3295803 0.1105732 mean_wait_time_doctor
12 3.4126731 4.6834229 0.8528233 4.1415648 5.2252810 0.1156970 mean_wait_time_doctor
13 4.8910189 4.6993918 0.8185437 4.2047508 5.1940328 0.1052564 mean_wait_time_doctor
14 3.4921984 4.6131637 0.8500401 4.1223651 5.1039622 0.1063909 mean_wait_time_doctor
15 3.8903965 4.5649792 0.8401085 4.0997426 5.0302158 0.1019143 mean_wait_time_doctor
16 2.9905528 4.4665776 0.9020290 3.9859202 4.9472349 0.1076120 mean_wait_time_doctor
17 5.3595945 4.5191080 0.8998408 4.0564525 4.9817634 0.1023776 mean_wait_time_doctor
18 3.8887614 4.4840887 0.8855267 4.0437267 4.9244508 0.0982055 mean_wait_time_doctor
19 3.6892115 4.4422531 0.8796859 4.0182580 4.8662481 0.0954459 mean_wait_time_doctor
20 4.2884182 4.4345613 0.8569141 4.0335132 4.8356095 0.0904369 mean_wait_time_doctor
21 4.3597185 4.4309974 0.8353762 4.0507387 4.8112561 0.0858179 mean_wait_time_doctor
22 3.8827551 4.4060773 0.8235803 4.0409222 4.7712323 0.0828753 mean_wait_time_doctor
23 4.6397718 4.4162379 0.8061191 4.0676459 4.7648299 0.0789342 mean_wait_time_doctor
1 0.6832362 0.6832362 NA NA NA NA utilisation_doctor
2 0.7014341 0.6923351 NA NA NA NA utilisation_doctor
3 0.6503975 0.6783559 0.0258659 0.6141014 0.7426104 0.0947210 utilisation_doctor
4 0.6437990 0.6697167 0.0272869 0.6262971 0.7131363 0.0648327 utilisation_doctor
5 0.6789189 0.6715571 0.0239868 0.6417735 0.7013407 0.0443500 utilisation_doctor
6 0.6713653 0.6715251 0.0214546 0.6490099 0.6940404 0.0335285 utilisation_doctor
7 0.6775094 0.6723800 0.0197155 0.6541463 0.6906138 0.0271182 utilisation_doctor
8 0.6528520 0.6699390 0.0195151 0.6536240 0.6862541 0.0243530 utilisation_doctor
1 1.2047321 1.2047321 NA NA NA NA mean_queue_length_doctor
2 1.0585763 1.1316542 NA NA NA NA mean_queue_length_doctor
3 1.0061322 1.0898135 0.1029189 0.8341487 1.3454783 0.2345950 mean_queue_length_doctor
4 0.7220796 0.9978800 0.2021598 0.6761987 1.3195614 0.3223648 mean_queue_length_doctor
5 0.7147191 0.9412479 0.2160728 0.6729580 1.2095377 0.2850363 mean_queue_length_doctor
6 0.9998528 0.9510153 0.1947367 0.7466517 1.1553790 0.2148900 mean_queue_length_doctor
7 0.9630582 0.9527358 0.1778278 0.7882725 1.1171990 0.1726221 mean_queue_length_doctor
8 0.9401393 0.9511612 0.1646967 0.8134713 1.0888511 0.1447598 mean_queue_length_doctor
9 0.9319599 0.9490277 0.1541926 0.8305048 1.0675506 0.1248888 mean_queue_length_doctor
10 1.2095963 0.9750846 0.1671025 0.8555466 1.0946225 0.1225924 mean_queue_length_doctor
11 0.8724811 0.9657570 0.1615177 0.8572479 1.0742660 0.1123565 mean_queue_length_doctor
12 0.6465119 0.9391532 0.1794699 0.8251235 1.0531830 0.1214176 mean_queue_length_doctor
13 0.9578633 0.9405925 0.1719077 0.8367097 1.0444752 0.1104440 mean_queue_length_doctor
14 0.7166333 0.9245954 0.1756750 0.8231637 1.0260271 0.1097039 mean_queue_length_doctor
15 0.7937702 0.9158737 0.1726219 0.8202789 1.0114685 0.1043755 mean_queue_length_doctor
16 0.5950870 0.8958245 0.1850493 0.7972187 0.9944304 0.1100727 mean_queue_length_doctor
17 1.0952642 0.9075563 0.1855878 0.8121358 1.0029767 0.1051400 mean_queue_length_doctor
18 0.7925600 0.9011676 0.1820754 0.8106236 0.9917116 0.1004741 mean_queue_length_doctor
19 0.7424607 0.8928146 0.1806527 0.8057428 0.9798864 0.0975251 mean_queue_length_doctor
20 0.8539327 0.8908705 0.1760492 0.8084769 0.9732641 0.0924866 mean_queue_length_doctor
21 0.8341843 0.8881712 0.1720368 0.8098609 0.9664814 0.0881702 mean_queue_length_doctor
22 0.7866429 0.8835562 0.1692804 0.8085015 0.9586110 0.0849462 mean_queue_length_doctor
23 0.9277437 0.8854774 0.1656448 0.8138472 0.9571076 0.0808944 mean_queue_length_doctor
24 0.7972331 0.8818006 0.1630022 0.8129708 0.9506304 0.0780559 mean_queue_length_doctor
1 15.5867030 15.5867030 NA NA NA NA mean_time_in_system
2 15.6470504 15.6168767 NA NA NA NA mean_time_in_system
3 14.8030177 15.3455904 0.4708495 14.1759353 16.5152455 0.0762209 mean_time_in_system
4 13.4202268 14.8642495 1.0366078 13.2147752 16.5137238 0.1109692 mean_time_in_system
5 13.4190380 14.5752072 1.1061844 13.2016978 15.9487166 0.0942360 mean_time_in_system
6 14.9968766 14.6454854 1.0042656 13.5915733 15.6993975 0.0719616 mean_time_in_system
7 15.0665982 14.7056444 0.9304792 13.8450947 15.5661941 0.0585183 mean_time_in_system
8 14.9253467 14.7331072 0.8649513 14.0099898 15.4562245 0.0490811 mean_time_in_system
9 14.2334536 14.6775901 0.8260523 14.0426301 15.3125501 0.0432605 mean_time_in_system
10 16.5390912 14.8637402 0.9762495 14.1653734 15.5621070 0.0469846 mean_time_in_system
1 3.2207992 3.2207992 NA NA NA NA mean_patients_in_system
2 3.2002959 3.2105475 NA NA NA NA mean_patients_in_system
3 2.9105293 3.1105415 0.1735187 2.6794971 3.5415858 0.1385753 mean_patients_in_system
4 2.6581309 2.9974388 0.2669107 2.5727244 3.4221533 0.1416925 mean_patients_in_system
5 2.7277981 2.9435107 0.2607148 2.6197905 3.2672309 0.1099776 mean_patients_in_system
6 3.0399497 2.9595838 0.2364907 2.7114021 3.2077656 0.0838570 mean_patients_in_system
7 2.9924023 2.9642722 0.2162415 2.7642821 3.1642623 0.0674668 mean_patients_in_system
8 2.9064020 2.9570384 0.2012436 2.7887946 3.1252822 0.0568961 mean_patients_in_system
9 2.9145095 2.9523130 0.1887791 2.8072045 3.0974215 0.0491508 mean_patients_in_system
10 3.2673469 2.9838164 0.2039668 2.8379073 3.1297255 0.0489002 mean_patients_in_system
11 2.7941860 2.9665773 0.2017704 2.8310261 3.1021284 0.0456928 mean_patients_in_system


We can use the function plot_replication_ci from above again to create the plots.

plot_replication_ci(
  conf_ints = filter(alg$summary_table, metric == "mean_wait_time_doctor"),
  yaxis_title = "Mean wait time",
  min_rep = alg$nreps[["mean_wait_time_doctor"]]
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

plot_replication_ci(
  conf_ints = filter(alg$summary_table, metric == "utilisation_doctor"),
  yaxis_title = "Mean utilisation",
  min_rep = alg$nreps[["utilisation_doctor"]]
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

plot_replication_ci(
  conf_ints = filter(alg$summary_table, metric == "mean_queue_length_doctor"),
  yaxis_title = "Mean queue length",
  min_rep = alg$nreps[["mean_queue_length_doctor"]]
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

plot_replication_ci(
  conf_ints = filter(alg$summary_table, metric == "mean_time_in_system"),
  yaxis_title = "Mean time in system",
  min_rep = alg$nreps[["mean_time_in_system"]]
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

plot_replication_ci(
  conf_ints = filter(alg$summary_table, metric == "mean_patients_in_system"),
  yaxis_title = "Mean patients in system",
  min_rep = alg$nreps[["mean_patients_in_system"]]
)
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_ribbon()`).

Explore the example models

Nurse visit simulation

GitHub Click to visit pydesrap_mms repository

Key files simulation/SimulationAdapter
notebooks/choosing_replications.ipynb
What to look for? Runs the manual and automated methods, as on this page. Includes a sensitivity analysis which checks the stability of the suggested number of replications, achieved by adding a seed_offset parameter that can be used to create a new set of seeds. The variation observed in the sensitivity analysis influences the chosen number of replications, and this is worth being aware of, if you also find yourself with a simulation with a relatively low suggested number of replications.

GitHub Click to visit rdesrap_mms repository

Key files R/choose_replications.R
rmarkdown/choosing_replications.md
What to look for? Runs the manual and automated methods, as on this page. Includes a sensitivity analysis which checks the stability of the suggested number of replications, achieved by adding a seed_offset parameter that can be used to create a new set of seeds. The variation observed in the sensitivity analysis influences the chosen number of replications, and this is worth being aware of, if you also find yourself with a simulation with a relatively low suggested number of replications.

Stroke pathway simulation

Not relevant - replicating an existing model described in a paper, so just used the number of replications stated by the authors.

Test yourself

Have a go for yourself!

Try out both the manual and automated methods described above to work out how many replications you need for your own simulation model.

See what happens if you change model parameters like run length - notice how this affects the recommended number of replications.