5 Reproduction

5.1 Studies

Shoaib and Ramamohan (2021): Uses python (salabim) to model primary health centres (PHCs) in India. The model has four patient types: outpatients, inpatients, childbirth cases and antenatal care patients. Four model configurations are developed based on observed PHC practices or government-mandated operational guidelines. The paper explores different operational patterns for scenarios where very high utilisation was observed, to explore what might help reduce utilisation of these resources. Note: The article was as Shoaib and Ramamohan (2022), but we used the green open access pre-print Shoaib and Ramamohan (2021). Link to reproduction.

Huang et al. (2019): Uses R (simmer) to model an endovascular clot retrieval (ECR) service. ECR is a treatment for acute ischaemic stroke. The model includes the stroke pathway, as well as three other pathways that share resources with the stroke pathway: an elective non-stroke interventional neuroradiology pathway, an emergency interventional radiology pathway, and an elective interventional radiology pathway. The paper explores waiting times and resource utilisation - particularly focussing on the biplane angiographic suite (angioINR). A few scenarios are tried to help examine why the wait times are so high for the angioINR. Link to reproduction.

Lim et al. (2020): Uses python (NumPy and pandas) to model the transmission of COVID-19 in a laboratory. It examines the proportion of staff infected in scenarios varying the: number of shifts per day; number of staff per shift; overall staff pool; shift patterns; secondary attack rate of the virus; introduction of protective measures (social distancing and personal protective equipment). Link to reproduction.

Kim et al. (2021): Adapts a previously developed R (Rcpp, expm, msm, foreach, iterators, doParallel) model for abdominal aortic aneurysm (AAA) screening of men in England. The model is adapted/used to explore different approaches to resuming screening and surgical repair for AAA, as these services were paused or substantially reduced during COVID-19 due to concerns about virus transmission. Link to reproduction.

Anagnostou et al. (2022): This paper includes two models - we have focussed just on the dynamiC Hospital wARd Management (CHARM) model. CHARM uses python (SimPy) to model intensive care units (ICU) in the COVID-19 pandemic (as well as subsequent stays in a recovery bed). It includes three types of admission to the ICU (emergency, elective or COVID-19). COVID-19 patients are kept seperate, and if they run out of capacity due to a surge in COVID-19 admissions, additional capacity can be pooled from the elective and emergency capacity. Link to reproduction.

Johnson et al. (2021): This study uses a previously validated discrete-event simulation model, EPIC: Evaluation Platform in chronic obstructive pulmonary disease (COPD). The model is written in C++ with an R interface, using R scripts for execution. The model is adapted to evaluate the cost-effectiveness of 16 COPD case detection strategies in primary care, comparing costs, quality-adjusted life years (QALYs), incremental cost-effectiveness ratios (ICER), and incremental net monetary benefits (INMB) across scenarios. Sensitivity analyses are also conducted. Link to reproduction.

Hernandez et al. (2015): This study models Points-of-Dispensing (PODs) in New York City. These are sites set up during a public health emergency to dispense counter-measures. The authors use evolutionary algorithms combined with discrete-event simulation to explore optimal staff numbers with regards to resource use, wait time and throughput. They use python for most of the analysis (with SimPy for the simulation component), but R to produce the plots and tables for the paper. Link to reproduction.

Wood et al. (2021): This study uses discrete-event simulation (R (base R, dplyr, tidyr)) to explore the deaths and life years lost under different triage strategies for an intensive care unit, relative to a baseline strategy. The unit is modelled with 20 beds (varied from 10 to 200 in sensitivity analyses). Three different triage strategies are explored, under three different projected demand trajectories. Link to reproduction.

5.2 Scope and reproduction

Study	Scope	Success	Time
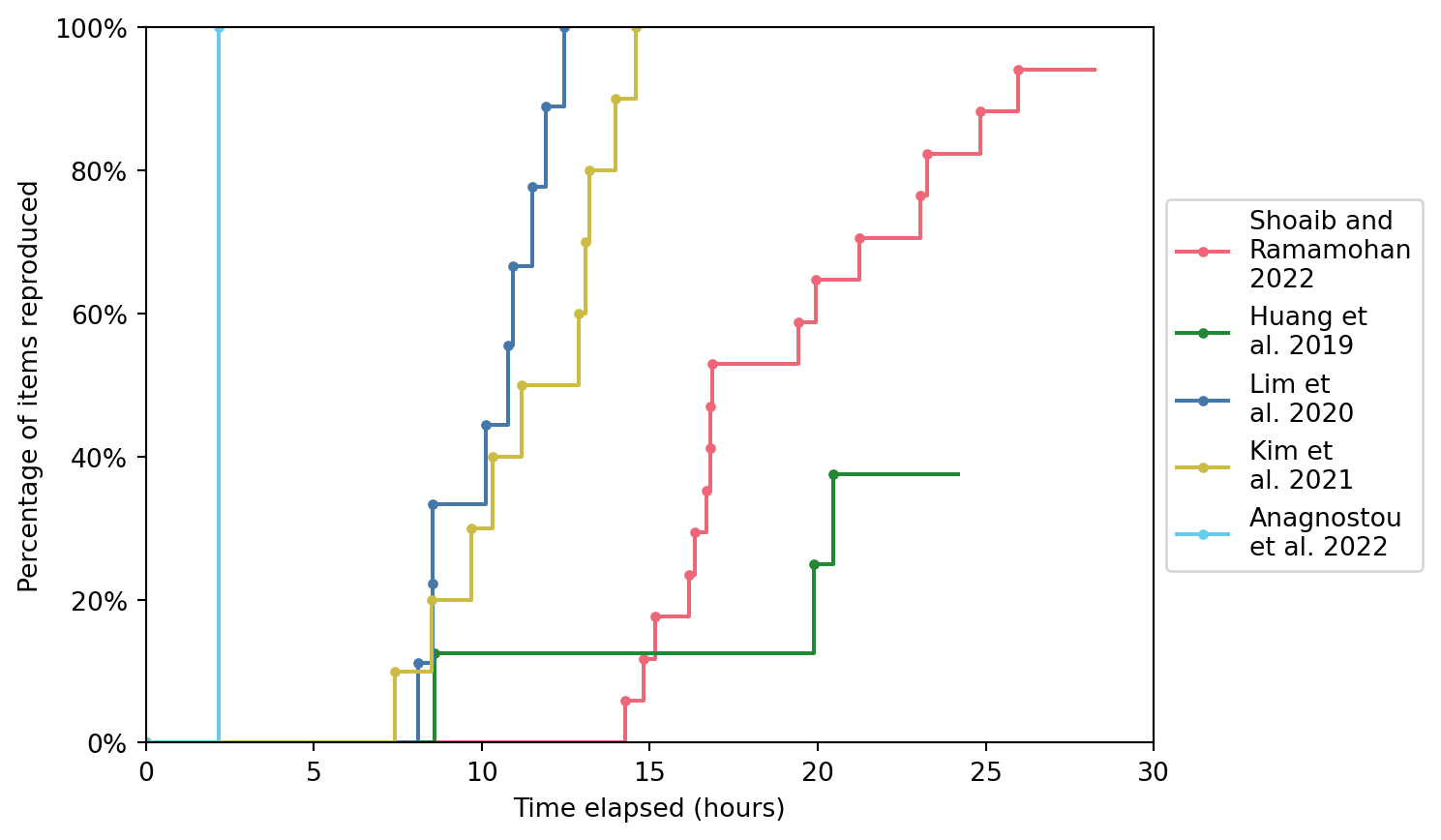
Shoaib and Ramamohan 2022	17 items: • 1 table • 9 figures • 7 in-text results	16 out of 17 (94.1%)	28h 14m
Huang et al. 2019	8 items: • 5 figures • 3 in-text results	3 out of 8 (37.5%)	24h 10m
Lim et al. 2020	9 items: • 5 tables • 4 figures	9 out of 9 (100%)	12h 27m
Kim et al. 2021	10 items: • 3 tables • 6 figures • 1 in-text result	10 out of 10 (100%)	14h 42m
Anagnostou et al. 2022	1 item: • 1 figure	1 out of 1 (100%)	2h 11m
Johnson et al. 2021	5 items: • 1 table • 4 figures	4 out of 5 (80%)	19h 49m
Hernandez et al. 2015	8 items: • 6 figures • 2 tables	1 out of 8 (12.5%)	17h 56m
Wood et al. 2021	5 items: • 4 figures • 1 table	5 out of 5 (100%)	3h 50m

Reproduction reflections

For the studies where I didn’t manage to fully reproduce results despite troubleshooting, my reflections on what I think to be the primary reason for not managing to reproduce results in each case were:

Shoaib and Ramamohan (2021): No specific suggestions - had to write code to run scenarios and process results, so it could be that I hadn’t done this all exactly the same as in the original study.

Huang et al. (2019): No specific suggestions - had to write code to run scenarios and process results, so it could be that I hadn’t done this all exactly the same as in the original study.

Johnson et al. (2021): No specific suggestions - although note that their results on GitHub appeared to likewise have the same discrepancy compared with the article, so it appears there might have been a minor change to the code/parameters made from that used to produce the article figure that might explain this.

Hernandez et al. (2015): This appears likely to be due to a parameter somewhere being not quite right. Ivan Hernandez suggested that it could be a random seed or that the optimisation doesn’t have enough runs - although was using the same seed and played around with run number. The other suggestion was that the version on GitHub might not have exactly the right version of inputs - and interestingly, he had an earlier version of the paper that had more similar results (our discrepancy was in range on Y axis, and he had an earlier version with range of 0 to 15000). This reaffirms that a minor parameter difference is the likely reason for the discrepancy, with that having impacted across nearly all the results.

5.3 Time to complete reproductions

Non-interactive figure:

Version of non-interactive figure used in article:

Interactive figure:

Timing reflections

There was a large amount of variation in the time each reproduction took. For each study, I have also reflected on what I think were the primary reasons behind things being quicker or slower:

Shoaib and Ramamohan (2021) - 28h 14m:

This had lots of items to reproduce (17)
Took me longer than usual to set up environment as needed specific package versions and had some confusion around package statistics which is base but I had mixed up with one that can be imported from conda/pypi
Most of the time was dedicated to identifying parameters for each scenario, writing code to run the scenarios (and run these programmatically), and writing code to process the results into figures and tables.

Huang et al. (2019) - 24h 10m:

Time-consuming aspects were modifying the code from the app so I could run it, writing code for each scenario, and writing code for figures (it took me quite a whiole to work out transformations for axes and how to standardise density)

Lim et al. (2020) - 12h 27m:

Lots of time was spent setting up model so could run programmatically, writing code for scenarios, and writing code to produce figures.

Kim et al. (2021) - 14h 42m:

Time-consuming aspect was largely writing code to produce tables and figures (including figuring out how to process).

Anagnostou et al. (2022) - 2h 11m:

This only had one item to reproduce.
It required very little troubleshooting - just had to write code to produce figure, although it was relatively simple.

Johnson et al. (2021) - 19h 49m:

Most time was spent on writing code for sensitivity analysis, and to produce tables and figures (which included working out which results tables / columns / scenarios to use, how to transform columns, and how to calculate features like efficiency frontier)

Hernandez et al. (2015) - 17h 56m:

Time-consuming aspects were writing code for scenarios and for figures and tables, and troubleshooting parameter discrepancies.

Wood et al. (2021) - 3h 50m:

Ran quick as code for model didn’t require troubleshooting (included all correct parameters and scenarios), and as they provided code to produce the figures and tables.

Regarding run time of the models themselves, for longer models, I sometimes experimented with parameters to run it quicker, in order to more easily troubleshoot, else I would run for a long time and then discover XYZ is wrong. Although the model run time itself is not included in the times, it is important to note, as some models took several days, and so in practice, this would impact on someone if they were trying to run a model within a short amount of time.

Regarding the reproduction run times, I think the main reflection from above is that including code with correct parameters and scenarios, and code to make the figures and tables, has a really big impact.

5.4 Model run times

For reference, the run times for the models are detailed below. It’s worth being aware that these are not compared on a “level playing field” as they were run on different machines, and with/without parallel processing or parallel terminals.

Study	Machine specs	Model run time	Additional details
Shoaib and Ramamohan (2021)	Intel Core i7-12700H with 32GB RAM running Ubuntu 22.04.4 Linux	22 minutes 26 seconds	This is based on the combined runtime of the notebooks which use 10 replications (rather than 100) and parallel processing, but with each notebook run seperately.
Huang et al. (2019)	Intel Core i7-12700H with 32GB RAM running Ubuntu 22.04.4 Linux	29 minutes 10 seconds	Combined time from notebooks run seperately.
Lim et al. (2020)	Intel Core i7-12700H with 32GB RAM running Ubuntu 22.04.4 Linux	49 minutes and 17 seconds
Kim et al. (2021)	Intel Core i9-13900K with 81GB RAM running Pop!_OS 22.04 Linux	6 hours 53 minutes	We reduced the number of patients in the simulation from 10 million to 1 million, to improve run times. Note, you can expect the runtime to be notably longer on machines with lower specs than this. For example, I ran surveillance scenario 0 on an Intel Core i7-12700H with 32GB RAM running Ubuntu 22.04.4 Linux. The runtime increased from 4 minutes 28 seconds up to 21 minutes 59 seconds.
Anagnostou et al. (2022)	Intel Core i7-12700H with 32GB RAM running Ubuntu 22.04.4 Linux	Only a few seconds.
Johnson et al. (2021)	Intel Core i9-13900K with 81GB RAM running Pop!_OS 22.04 Linux	At least 1 day 11 hours	It was run from the command line via multiple terminals simultaneously - hence, the exact times are impacted by the number being ran at once. The base case scenarios were ran at the same time, and took an overall total time of 20 hours 40 minutes. The sensitivity analysis scenario were all ran at the same time, and took an overall total of 1 day 10 hours 57 minutes. Four files (scenarios 2 and 3) had to be re-run seperately after fixing a mistake, and when just those were run, the total was 21 hours 26 minutes (quicker than when they were run as part of the full set of scenarios, when they took up to 1.3 days). Based on this, if you were to run all scenarios at once in parallel in seperate terminals, you could expect a run time of at least 1 day 11 hours, but would be higher than that (since the more run at once, the lower it takes, as you can see from the scenario 2 and 3 times above).
Hernandez et al. (2015)	Intel Core i9-13900K with 81GB RAM running Pop!_OS 22.04 Linux	9 hours 16 minutes	This involved running the models within each experiment in parallel, but each of the experiment files seperately. If these are run at the same time (which I could do without issue), then you will be able to run them all within 4 hours 28 minutes (the longest experiment) (or a little longer, due to slowing speeds from running at once). Also, this has excluded one of the variants for Experiment 3, which I did not run as it had a very long run time (quoted to be 27 hours in the article) and as, regardless, I had not managed to reproduce the other sub-plots in the figure for that experiment.
Wood et al. (2021)	Intel Core i9-13900K with 81GB RAM running Pop!_OS 22.04 Linux	48 hours 25 minutes	It ran in a single loop, so required the computer to remain on for that time. This time includes all scenarios - but, for just the base scenario, the run time was 2 hours 3 minutes.

5.5 References

Anagnostou, Anastasia, Derek Groen, Simon J. E. Taylor, Diana Suleimenova, Nura Abubakar, Arindam Saha, Kate Mintram, et al. 2022. “FACS-CHARM: A Hybrid Agent-Based and Discrete-Event Simulation Approach for Covid-19 Management at Regional Level.” In 2022 Winter Simulation Conference (WSC), 1223–34. https://doi.org/10.1109/WSC57314.2022.10015462.

Hernandez, Ivan, Jose E. Ramirez-Marquez, David Starr, Ryan McKay, Seth Guthartz, Matt Motherwell, and Jessica Barcellona. 2015. “Optimal Staffing Strategies for Points of Dispensing.” Computers & Industrial Engineering 83 (May): 172–83. https://doi.org/10.1016/j.cie.2015.02.015.

Huang, Shiwei, Julian Maingard, Hong Kuan Kok, Christen D. Barras, Vincent Thijs, Ronil V. Chandra, Duncan Mark Brooks, and Hamed Asadi. 2019. “Optimizing Resources for Endovascular Clot Retrieval for Acute Ischemic Stroke, a Discrete Event Simulation.” Frontiers in Neurology 10 (June). https://doi.org/10.3389/fneur.2019.00653.

Johnson, Kate M., Mohsen Sadatsafavi, Amin Adibi, Larry Lynd, Mark Harrison, Hamid Tavakoli, Don D. Sin, and Stirling Bryan. 2021. “Cost Effectiveness of Case Detection Strategies for the Early Detection of COPD.” Applied Health Economics and Health Policy 19 (2): 203–15. https://doi.org/10.1007/s40258-020-00616-2.

Kim, Lois G., Michael J. Sweeting, Morag Armer, Jo Jacomelli, Akhtar Nasim, and Seamus C. Harrison. 2021. “Modelling the Impact of Changes to Abdominal Aortic Aneurysm Screening and Treatment Services in England During the COVID-19 Pandemic.” PLOS ONE 16 (6): e0253327. https://doi.org/10.1371/journal.pone.0253327.

Lim, Chun Yee, Mary Kathryn Bohn, Giuseppe Lippi, Maurizio Ferrari, Tze Ping Loh, Kwok-Yung Yuen, Khosrow Adeli, and Andrea Rita Horvath. 2020. “Staff Rostering, Split Team Arrangement, Social Distancing (Physical Distancing) and Use of Personal Protective Equipment to Minimize Risk of Workplace Transmission During the COVID-19 Pandemic: A Simulation Study.” Clinical Biochemistry 86 (December): 15–22. https://doi.org/10.1016/j.clinbiochem.2020.09.003.

Shoaib, Mohd, and Varun Ramamohan. 2021. “Simulation Modelling and Analysis of Primary Health Centre Operations.” arXiv, June. https://doi.org/10.48550/arXiv.2104.12492.

———. 2022. “Simulation Modeling and Analysis of Primary Health Center Operations.” SIMULATION 98 (3): 183–208. https://doi.org/10.1177/00375497211030931.

Wood, Richard M., Adrian C. Pratt, Charlie Kenward, Christopher J. McWilliams, Ross D. Booton, Matthew J. Thomas, Christopher P. Bourdeaux, and Christos Vasilakis. 2021. “The Value of Triage During Periods of Intense COVID-19 Demand: Simulation Modeling Study.” Medical Decision Making 41 (4): 393–407. https://doi.org/10.1177/0272989X21994035.