Chose a seed that produced fairly similar figures to paper. Decided that each figure had now been successfully reproduced. Total time used: 7h 6m (17.8%).
Made changes to sim_replicate.py:
multiple_replications() to accept a base number, so the random number set is the replication number plus the base numberrun_replications() to accept base number to function, and input this to call of multiple_replications()Started changing end_trial_analysis.py to enable the function to accept changes to the filename, but then decided a simpler solution (that doesn’t require changing their code in multiple places) is just to use os.rename() within our notebook. Set up notebook to run through 15 different base seeds. Paused timing whilst this ran…
Looked over images, but all looked very similar to one another. Realised this was because my method for modifying the seeds still had lots of matching seeds between each run - for example:
Hence, changed this in reproduction.ipynb so the base numbers were 0, 100, 200, 300 etc, and so:
Then paused timing as reran again…
Compared against paper figures. Figures 2 and 3 always generally look quite consistent. Figure 4 can look quite different, and from the runs I’ve done, you can spot for example that our peaks in the left figure, and in the maximum of the right figure, often look lower.
Trying again with another set of 15, this time 1500 to 2900.
An alternative to this would be to identify the number of replications required for stable results - but that feels like less of a focus on reproducibility, and more of a focus on valid results.
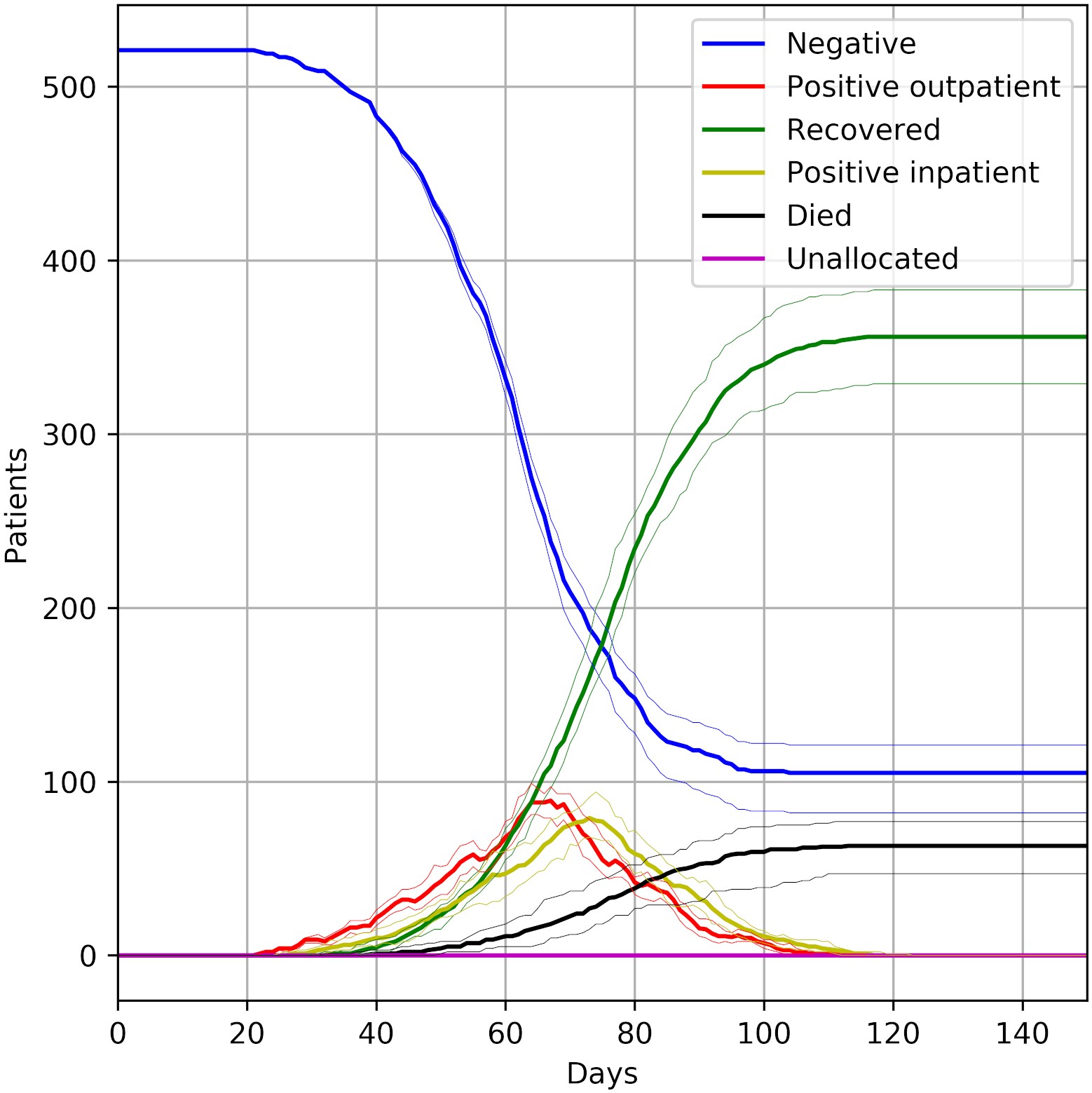
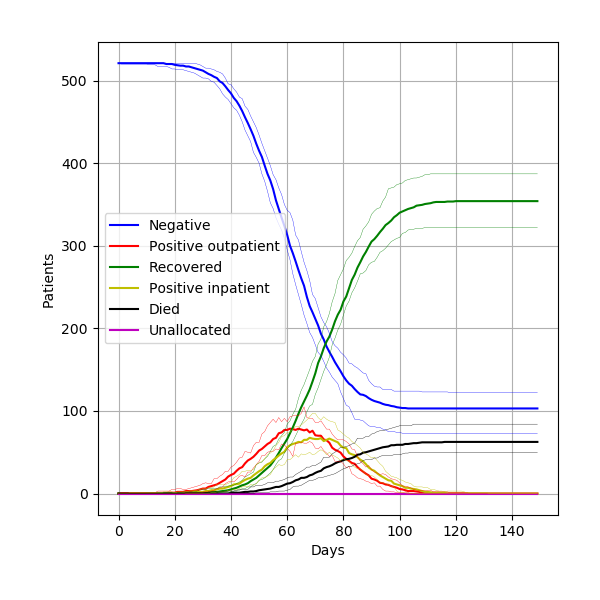
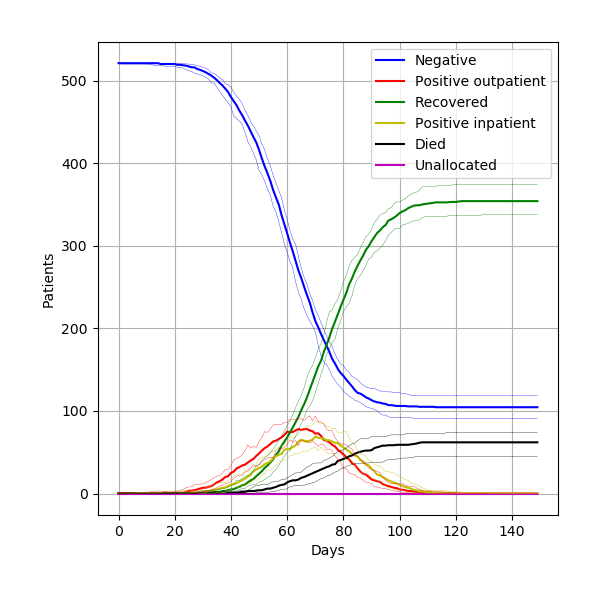
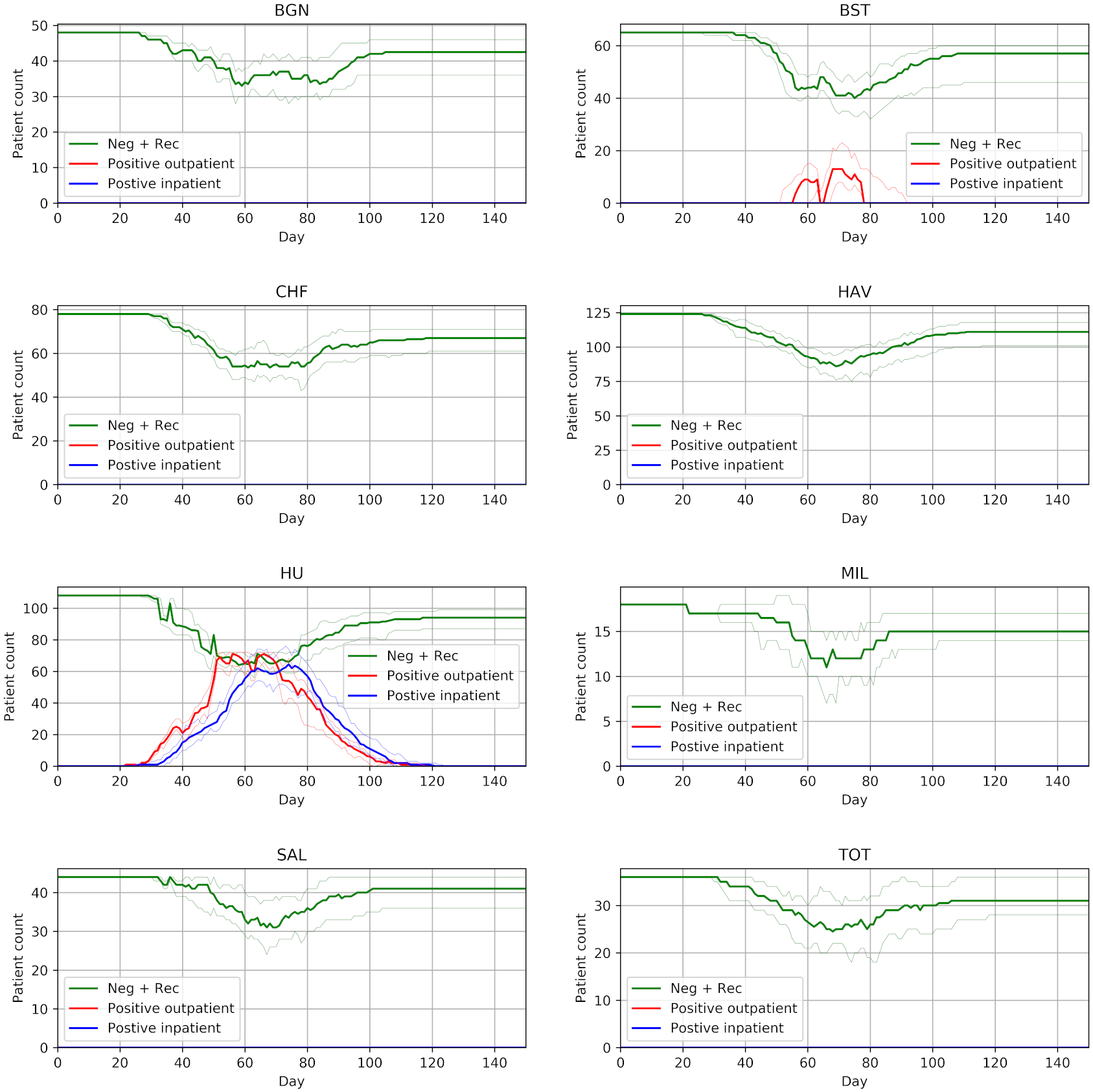
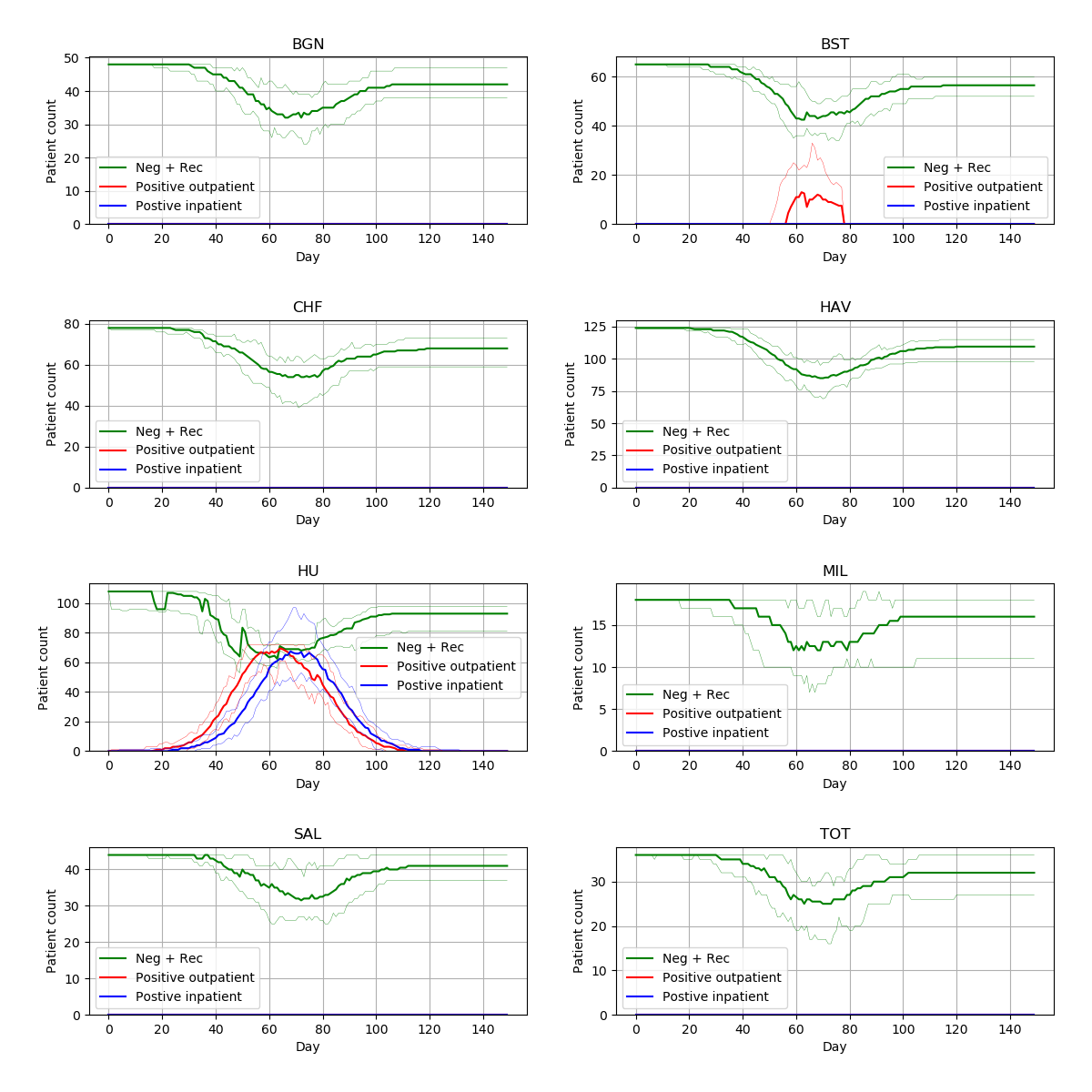
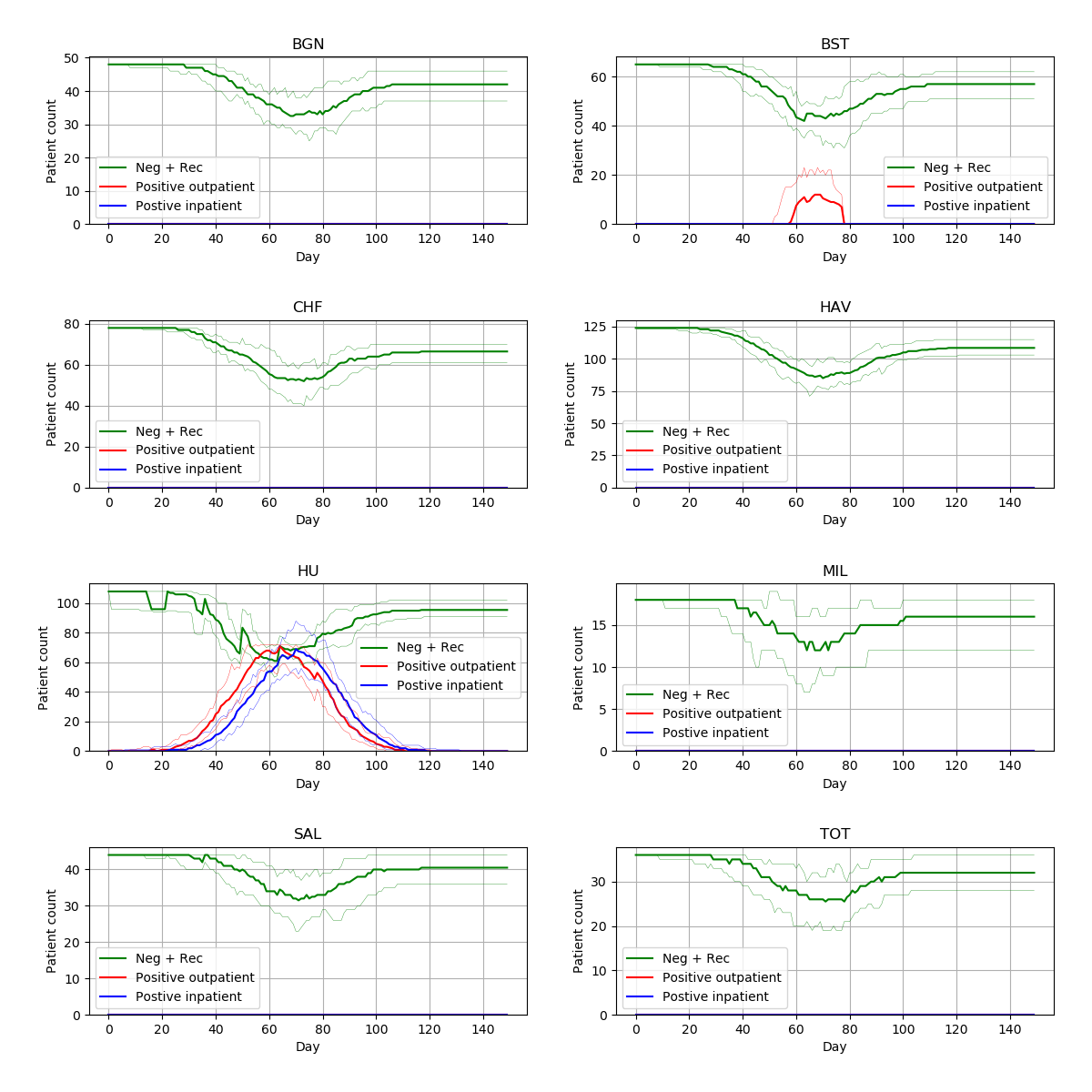
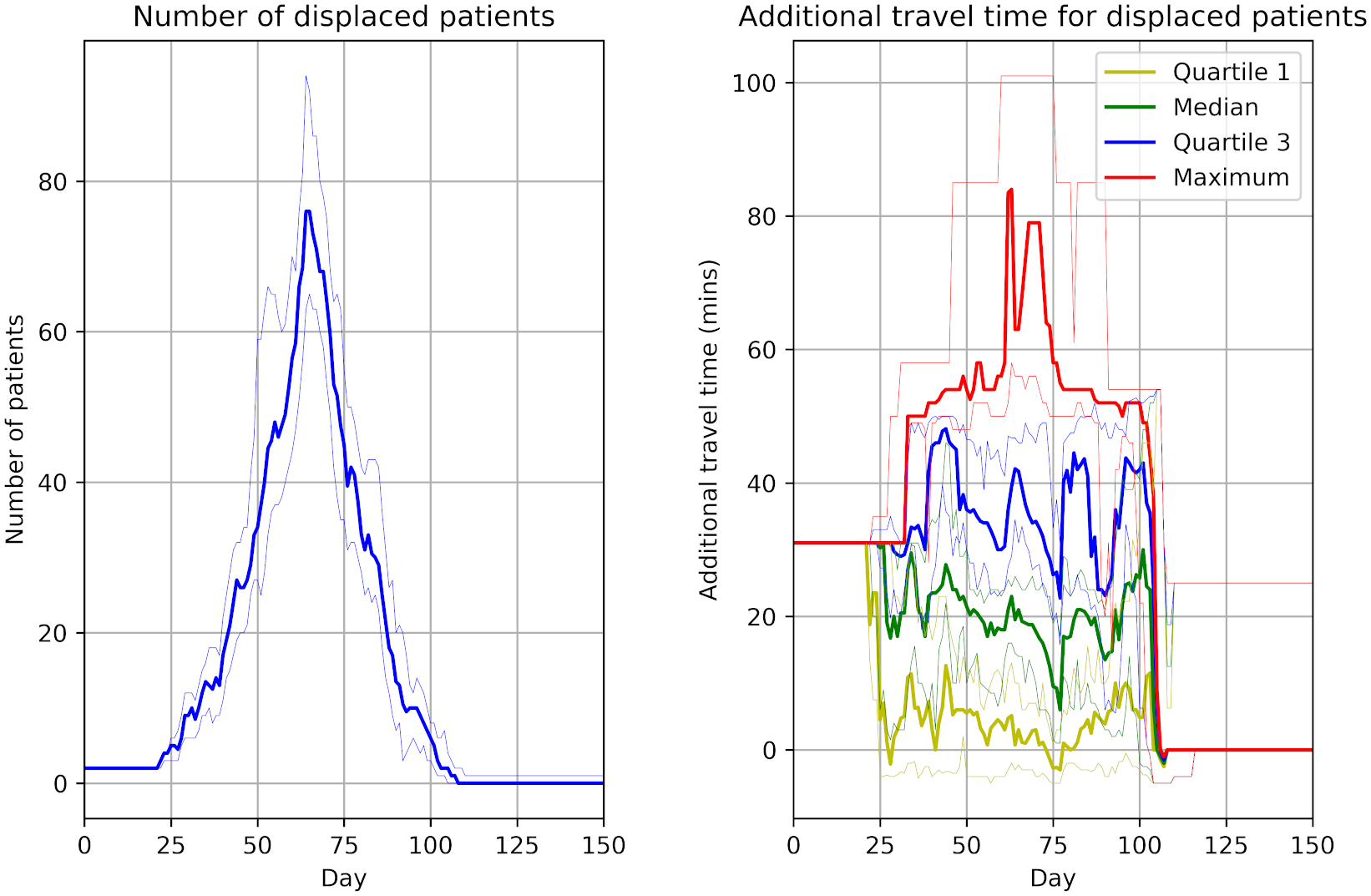
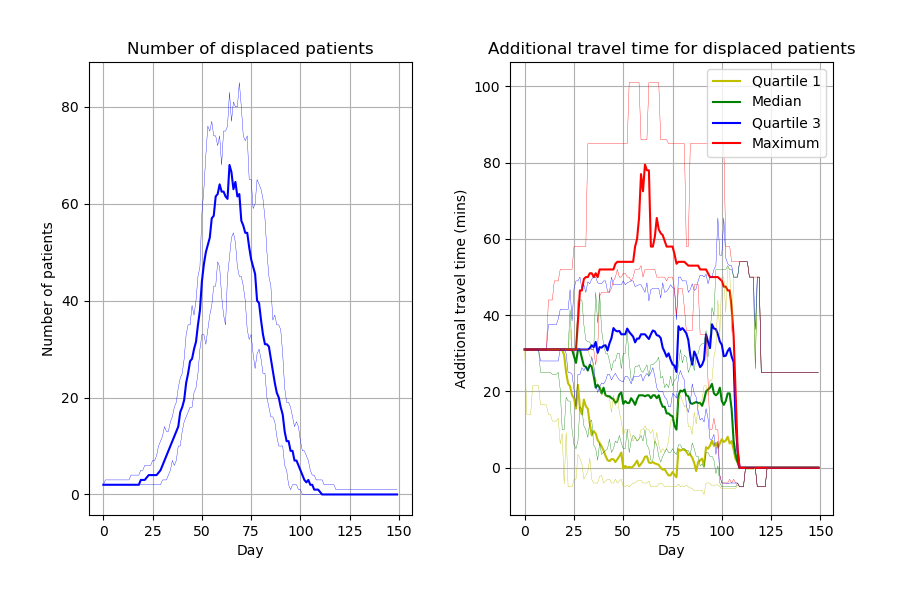
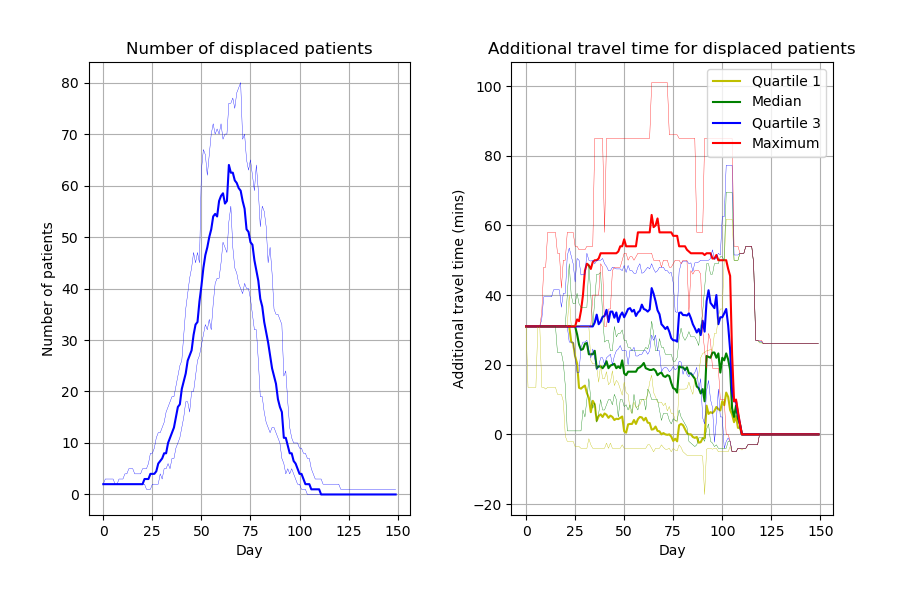
From 15 different versions, I’m finding the peaks of the figures from the paper to be slightly higher than typical. Assuming that model parameters are correct and that control of randomness is now implemented appropriately, this highlights the relevance of simulation stability. Although 30 replications were performed, there was not assessment of whether this was the number needed for stability of results. This might be relevant to consider for STARS framework.
As in ‘Simulation: The Practice of Model Development and Use’ by Stewart Robinson, there are three approaches for selecting the number of replications:
Still none with similar blue peak, but decided appropriate number of different seeds have now been tried. From visual comparison, felt base of 2700 produced results that were fairly visually similar - but from looking across them all, often there wasn’t alot between them.
Here are comparisons of:
Examples of differences to spot between them:
As I believe the parameters are consistent with the paper (as checked on Day 2), and as the models successfully run and produce broadly similar figures (with differences believed to be due to randomness/seeds, and related to simulation stability with this number of replications), I hence believe that at this point, reproduction is complete, and that each of these figures can be considered a successful reproduction.
Simplified the reproduction notebook to just use the base number 2700, deleting the other results.
Created a reproduction success page, presenting those figures alongside the figures from the original study.
Not archiving on Zenodo as this is the test-run.
import sys
sys.path.append('../')
from timings import calculate_times
# Minutes used prior to today
used_to_date = 345
# Times from today
times = [
('10.30', '11.03'),
('11.29', '11.36'),
('11.56', '12.00'),
('12.19', '12.45'),
('16.13', '16.24')]
# Print time used and remaining
calculate_times(used_to_date, times)Time spent today: 81m, or 1h 21m
Total used to date: 426m, or 7h 6m
Time remaining: 1974m, or 32h 54m
Used 17.8% of 40 hours max✅ = Made the change.
Protocol: