Scope

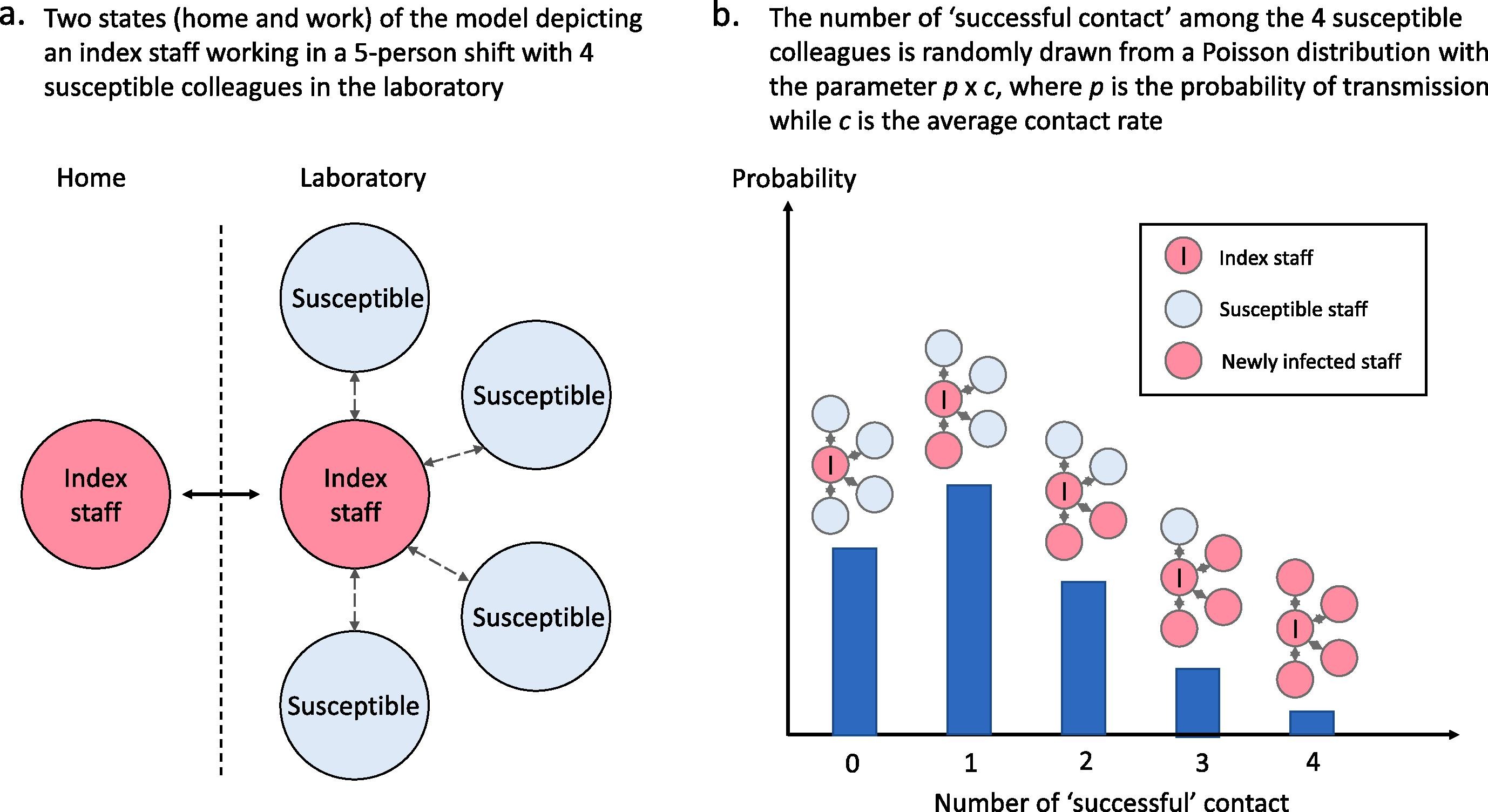
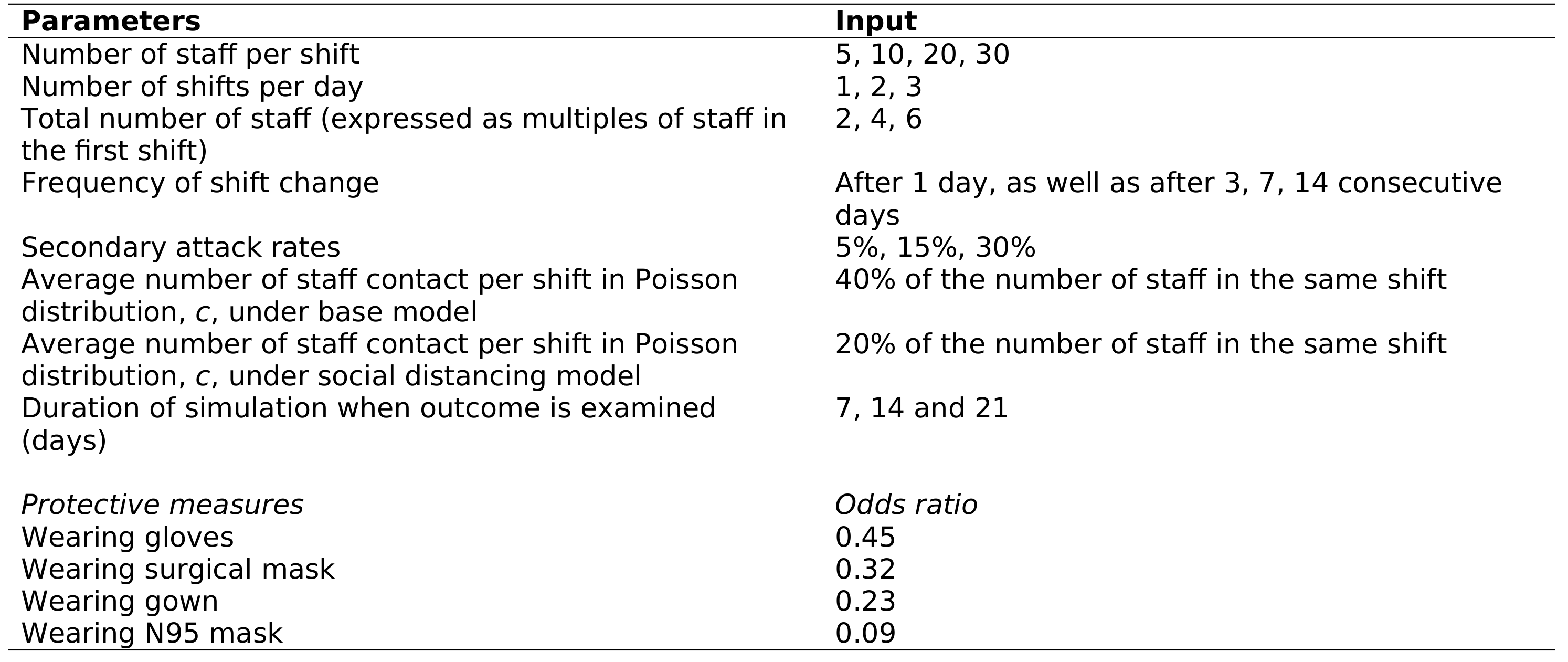
This page outlines the parts of the journal article which we will attempt to reproduce.

All images and quotes on this page are sourced from Lim et al. (2020)

Within scope

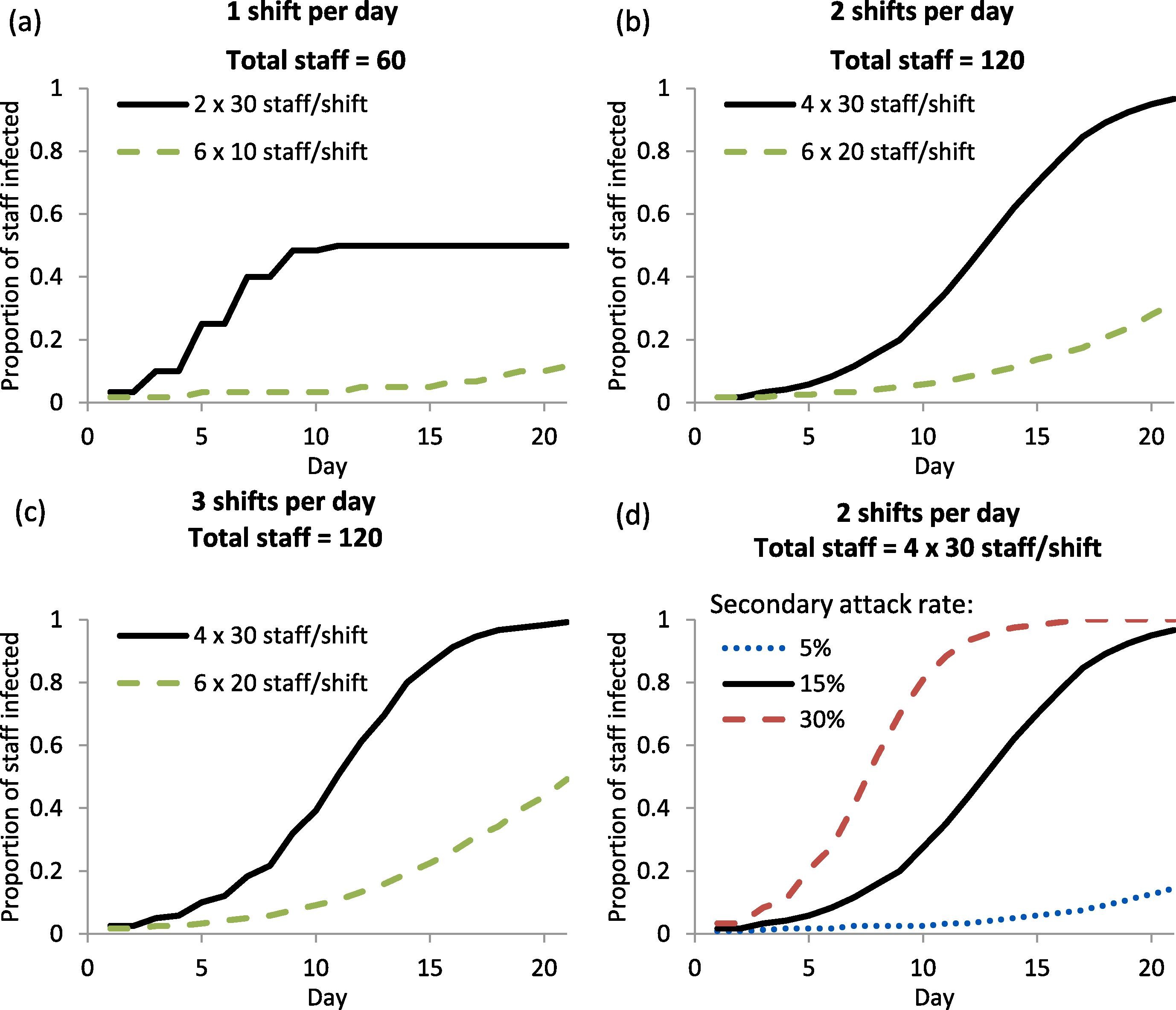
Figure 2. “Panels a, b and c show impact of different roster arrangements (number of shifts, number of staff per shift, total staff pool) on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with the stimulated staff working non-consecutive days. Panel d shows the effect of different secondary attack rates on proportion of staff infected.” Lim et al. (2020)

Figure 2. “Panels a, b and c show impact of different roster arrangements (number of shifts, number of staff per shift, total staff pool) on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with the stimulated staff working non-consecutive days. Panel d shows the effect of different secondary attack rates on proportion of staff infected.” Lim et al. (2020)

Figure 3. “Effect of number of staff per shift and of the number of shifts per day on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with the stimulated staff working non-consecutive days.” Lim et al. (2020)

Figure 3. “Effect of number of staff per shift and of the number of shifts per day on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with the stimulated staff working non-consecutive days.” Lim et al. (2020)

Figure 4. “Effect of frequency of shift change (i.e. number of consecutive days worked) on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with 20 staff per shift.” Lim et al. (2020)

Figure 4. “Effect of frequency of shift change (i.e. number of consecutive days worked) on the proportion of staff infected by workplace transmission. The secondary attack rate is set at 15% with 20 staff per shift.” Lim et al. (2020)

Figure 5. “Effect of a) split team arrangement, social distancing and b) personal protective equipment on the proportion of staff infected by workplace trans- mission. The data represents the impact of the individual interventions.” Lim et al. (2020)

Figure 5. “Effect of a) split team arrangement, social distancing and b) personal protective equipment on the proportion of staff infected by workplace trans- mission. The data represents the impact of the individual interventions.” Lim et al. (2020)

Supplemental Table 2. “Proportion of simulated laboratory staff infected by COVID-19 in base scenario with 15% probability of secondary infection at the end of day 7, day 14 and day 21 of the simulation. In this base scenario, the simulated staff worked fixed alternating workdays (i.e. fixed consecutive days on, and fixed minimum consecutive days off). The results shown are the median of 100 cycles of simulation. NA = not available as the number of staff per shift is too low to simulate under the required conditions.” Lim et al. (2020)

Reformatted table:

end_of_day shifts_per_day staff_per_shift strength staff_change prop_infected
0 7 1.0 5.0 2 1 0.20
1 7 1.0 5.0 2 3 0.20
2 7 1.0 5.0 2 7 0.30
3 7 1.0 5.0 2 14 0.40
4 7 1.0 5.0 2 21 0.30
... ... ... ... ... ... ...
535 21 3.0 30.0 6 1 0.80
536 21 3.0 30.0 6 3 0.78
537 21 3.0 30.0 6 7 0.39
538 21 3.0 30.0 6 14 0.17
539 21 3.0 30.0 6 21 0.17

540 rows × 6 columns

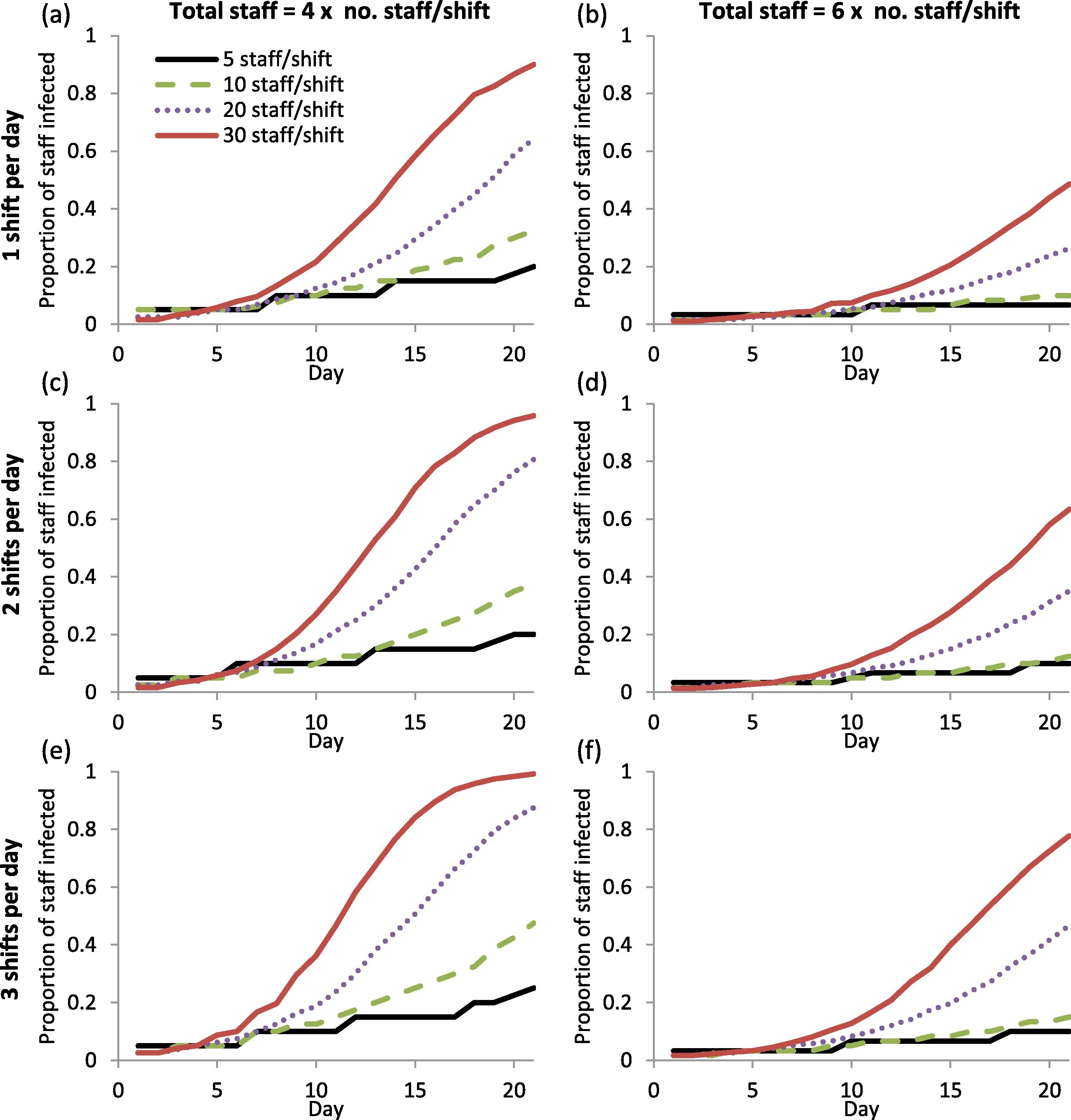
Supplemental Table 3. “Proportion of simulated laboratory staff infected by COVID-19 in base scenario with 5% probability of secondary infection at the end of day 7, day 14 and day 21 of the simulation. In this scenario, the simulated staff worked fixed alternating workdays (i.e. fixed consecutive days on, and fixed minimum consecutive days off). The results shown are the median of 100 cycles of simulation. NA = not available as the number of staff per shift was too low to simulate under the required conditions.” Lim et al. (2020)

Reformatted table:

end_of_day shifts_per_day staff_per_shift strength staff_change prop_infected
0 7 1.0 5.0 2 1 0.10
1 7 1.0 5.0 2 3 0.10
2 7 1.0 5.0 2 7 0.20
3 7 1.0 5.0 2 14 0.10
4 7 1.0 5.0 2 21 0.20
... ... ... ... ... ... ...
535 21 3.0 30.0 6 1 0.06
536 21 3.0 30.0 6 3 0.11
537 21 3.0 30.0 6 7 0.22
538 21 3.0 30.0 6 14 0.17
539 21 3.0 30.0 6 21 0.17

540 rows × 6 columns

Supplemental Table 4. “Proportion of simulated laboratory staff infected by COVID-19 in base scenario with 30% probability of secondary infection at the end of day 7, day 14 and day 21 of the simulation. In this scenario, the simulated staff worked fixed alternating workdays (i.e. fixed consecutive days on, and fixed minimum consecutive days off). The results shown are the median of 100 cycles of simulation. NA = not available as the number of staff per shift was too low to simulate under the required conditions.” Lim et al. (2020)

Reformatted table:

end_of_day shifts_per_day staff_per_shift strength staff_change prop_infected
0 7 1.0 5.0 2 1 0.40
1 7 1.0 5.0 2 3 0.30
2 7 1.0 5.0 2 7 0.50
3 7 1.0 5.0 2 14 0.50
4 7 1.0 5.0 2 21 0.50
... ... ... ... ... ... ...
535 21 3.0 30.0 6 1 0.99
536 21 3.0 30.0 6 3 0.91
537 21 3.0 30.0 6 7 0.39
538 21 3.0 30.0 6 14 0.17
539 21 3.0 30.0 6 21 0.17

540 rows × 6 columns

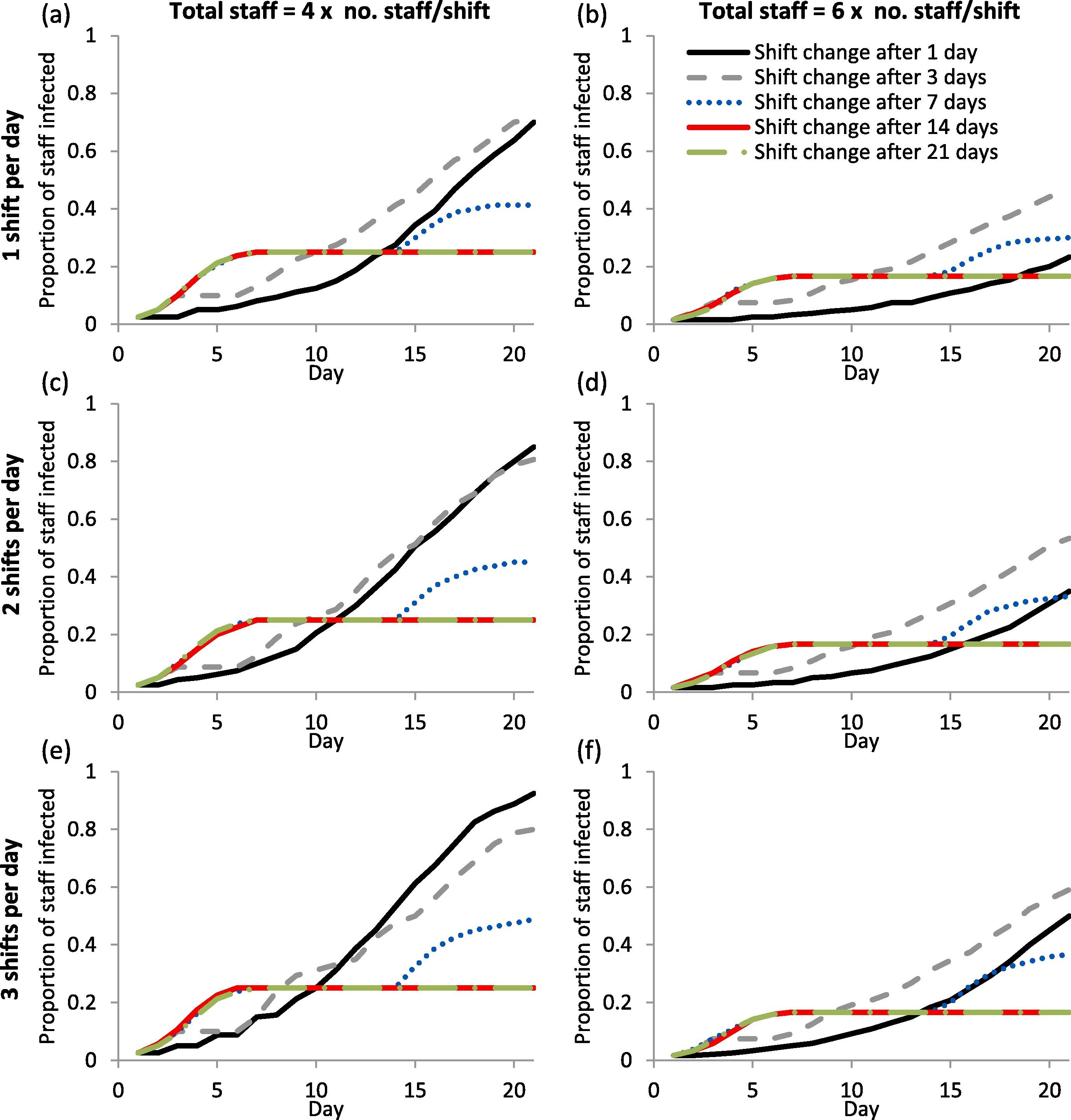
Supplemental Table 5. “Proportion of simulated laboratory staff working in a single shift infected by COVID-19 in a scenario with 15% probability of secondary infection at the end of day 7, day 14 and day 21 of the simulation without predefined minimum rest day (i.e. random shift assignment after each shift). The results shown are the median of 100 cycles of simulation.” Lim et al. (2020)

Reformatted table:

end_of_day shifts_per_day staff_per_shift strength staff_change prop_infected
0 7 1.0 5.0 2 1 0.25
1 7 1.0 5.0 2 3 0.30
2 7 1.0 5.0 2 7 0.30
3 7 1.0 5.0 2 14 0.30
4 7 1.0 5.0 2 21 0.40
... ... ... ... ... ... ...
175 21 1.0 30.0 6 1 0.59
176 21 1.0 30.0 6 3 0.67
177 21 1.0 30.0 6 7 0.42
178 21 1.0 30.0 6 14 0.31
179 21 1.0 30.0 6 21 0.17

180 rows × 6 columns

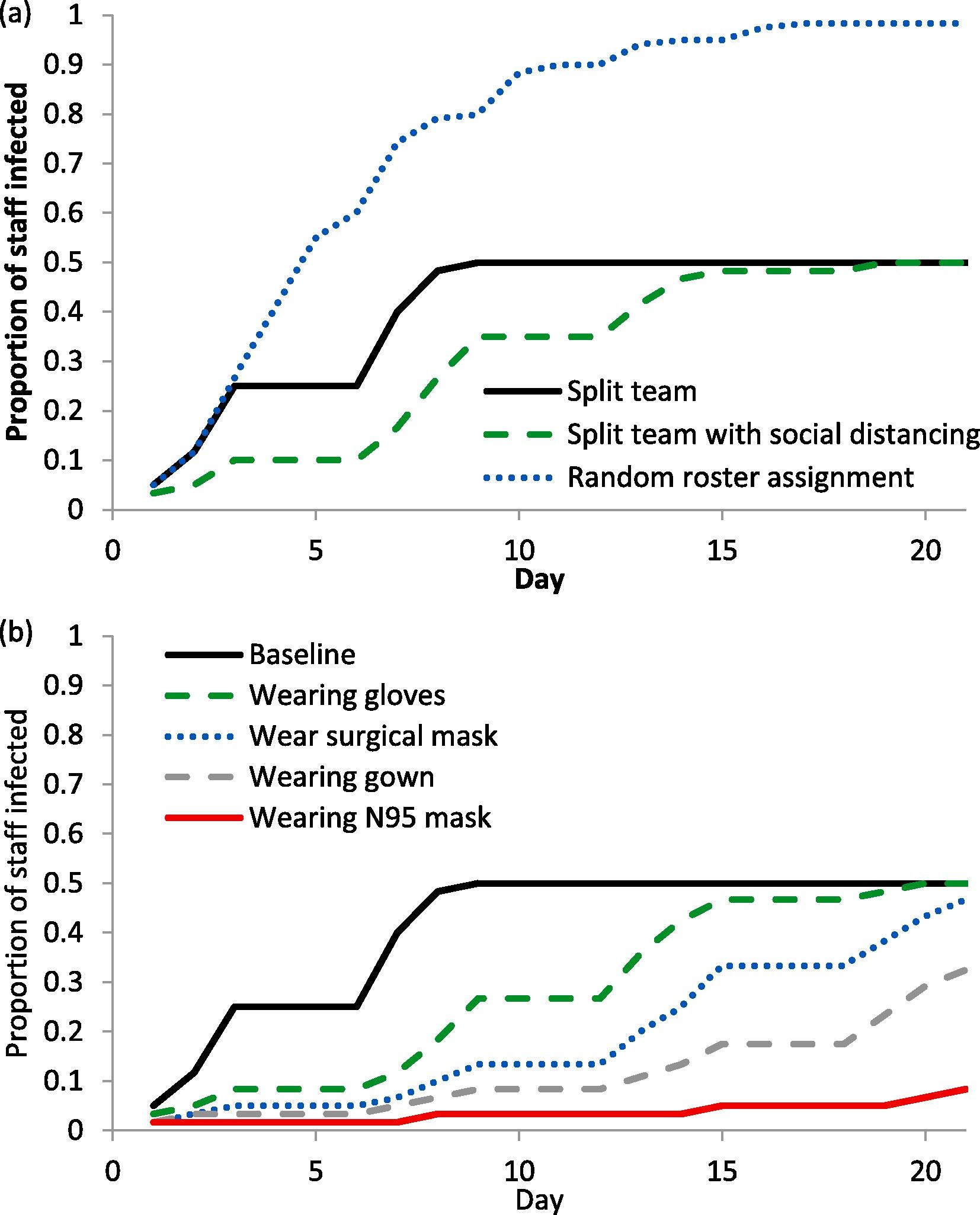
Supplemental Table 6. “Proportion of simulated laboratory staff infected by COVID-19 in base scenario with 15% probability of secondary infection at the end of day 14 of the simulation with the staff observing workplace social distancing (by reducing the contact rate by half) and using various personal protective equipment. In this scenario, the simulated staff worked fixed alternating workdays (i.e. fixed consecutive days on, and fixed minimum consecutive days off). The results shown are the median of 100 cycles of simulation. NA = not available as the number of staff per shift is too low to simulate under the required conditions.” Lim et al. (2020)

Reformatted table:

workplace_measure shifts_per_day staff_per_shift strength staff_change prop_infected
0 Gloves 1.0 5.0 2 1 0.20
1 Gloves 1.0 5.0 2 3 0.20
2 Gloves 1.0 5.0 2 7 0.20
3 Gloves 1.0 5.0 2 14 0.30
4 Gloves 1.0 5.0 2 21 0.30
... ... ... ... ... ... ...
895 Surgical mask 3.0 30.0 6 1 0.02
896 Surgical mask 3.0 30.0 6 3 0.05
897 Surgical mask 3.0 30.0 6 7 0.08
898 Surgical mask 3.0 30.0 6 14 0.16
899 Surgical mask 3.0 30.0 6 21 0.16

900 rows × 6 columns

Outside scope

Figure 1. “Visual representation of the simulation model. Panel a shows the two states a simulated staff can be in, namely staying at home or working in the laboratory with 4 colleagues (5-staff shift). Panel b shows the Poisson distribution from which the susceptible colleagues are drawn from”. Lim et al. (2020)

Figure 1. “Visual representation of the simulation model. Panel a shows the two states a simulated staff can be in, namely staying at home or working in the laboratory with 4 colleagues (5-staff shift). Panel b shows the Poisson distribution from which the susceptible colleagues are drawn from”. Lim et al. (2020)

Supplemental Table 1. “Key simulation parameters used in this study.” Lim et al. (2020)

Supplemental Table 1. “Key simulation parameters used in this study.” Lim et al. (2020)

References

Lim, Chun Yee, Mary Kathryn Bohn, Giuseppe Lippi, Maurizio Ferrari, Tze Ping Loh, Kwok-Yung Yuen, Khosrow Adeli, and Andrea Rita Horvath. 2020. “Staff Rostering, Split Team Arrangement, Social Distancing (Physical Distancing) and Use of Personal Protective Equipment to Minimize Risk of Workplace Transmission During the COVID-19 Pandemic: A Simulation Study.” Clinical Biochemistry 86 (December): 15–22. https://doi.org/10.1016/j.clinbiochem.2020.09.003.